ToNumberField[a,θ]
expresses the algebraic number a in the number field generated by θ.
ToNumberField[{a1,a2,…},θ]
expresses the ai in the field generated by θ.
ToNumberField[{a1,a2,…}]
expresses the ai in a common extension field generated by a single algebraic number.


ToNumberField
ToNumberField[a,θ]
expresses the algebraic number a in the number field generated by θ.
ToNumberField[{a1,a2,…},θ]
expresses the ai in the field generated by θ.
ToNumberField[{a1,a2,…}]
expresses the ai in a common extension field generated by a single algebraic number.
Details

- ToNumberField gives AlgebraicNumber objects corresponding to elements of the rational extension
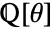 .
. - ToNumberField[a,θ] remains unevaluated if a does not exist in
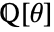 .
. - The ai and θ can be given in terms of Root or AlgebraicNumber objects, or ordinary rationals and radicals.
- If θ is an algebraic integer the results will always be given in terms of AlgebraicNumber[θ,list].
- ToNumberField[{a1,a2,…}] gives a representation of the ai in terms of a primitive element of the field
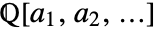 .
. - ToNumberField[{a1,a2,…}] is equivalent to ToNumberField[{a1,a2,…},Automatic], and does not necessarily use the smallest common field extension.
- ToNumberField[{a1,a2,…},All] always uses the smallest common field extension.
- ToNumberField[x] converts any form of algebraic number to an explicit AlgebraicNumber object.
Examples
open all close allScope (6)
The generator θ of the number field will autoreduce to an algebraic integer:
Root objects:
AlgebraicNumber objects:
Express ![]() and
and ![]() in a common extension field:
in a common extension field:
Express algebraic numbers in the smallest common extension field:
Properties & Relations (1)
Convert an algebraic number to an explicit AlgebraicNumber object:
Tech Notes
Related Guides
History
Text
Wolfram Research (2007), ToNumberField, Wolfram Language function, https://reference.wolfram.com/language/ref/ToNumberField.html.
CMS
Wolfram Language. 2007. "ToNumberField." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ToNumberField.html.
APA
Wolfram Language. (2007). ToNumberField. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ToNumberField.html
BibTeX
@misc{reference.wolfram_2025_tonumberfield, author="Wolfram Research", title="{ToNumberField}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/ToNumberField.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_tonumberfield, organization={Wolfram Research}, title={ToNumberField}, year={2007}, url={https://reference.wolfram.com/language/ref/ToNumberField.html}, note=[Accessed: 10-March-2026]}