gives the Frobenius decomposition of a square matrix a as a list {s,c}, such that 
where s is a similarity matrix and c is a block companion diagonal matrix.
FrobeniusDecomposition
gives the Frobenius decomposition of a square matrix a as a list {s,c}, such that 
where s is a similarity matrix and c is a block companion diagonal matrix.
Details
- FrobeniusDecomposition is also known as rational canonical decomposition or Frobenius canonical decomposition. The c matrix is the Frobenius normal form.
- FrobeniusDecomposition is typically used to analyze and solve systems of linear differential equations or linear difference equations.
- The characteristic polynomial
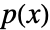of a above has the form 
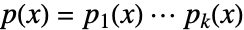, and each companion matrix ci=CompanionMatrix[{pi[x],x}]. Furthermore, 
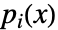divides 
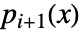, and also 
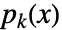is the MatrixMinimalPolynomial of a. - FrobeniusDecomposition[m] always exists for a matrix m; EigenvalueDecomposition[m] only exists if the JordanDecomposition[m] is diagonal.
- FrobeniusDecomposition uses only rational operations on the input, so is often a more efficient choice than JordanDecomposition.
- FrobeniusDecomposition works for exact and approximate matrices. However, it is numerically unstable, and for many numerical problems, the stable SchurDecomposition is a better choice.
Examples
open all close allBasic Examples (2)
Options (1)
Modulus (1)
FrobeniusDecomposition can work modulo a prime:
Properties & Relations (2)
Compute the Frobenius decomposition of a matrix:
The polynomial Smith reduction can be used to compute the rational canonical form of a matrix (the second element in the Frobenius decomposition).
Compute the Smith form of a characteristic matrix and extract the diagonal:
Obtain the diagonal elements of positive degree, corresponding to companion matrix polynomials:
Check the last one is the matrix minimal polynomial:
Check that their product is the matrix characteristic polynomial:
Use these to create companion matrix blocks:
Use SparseArray and Band to reconstruct the companion matrix for m as a diagonal block matrix:
Text
Wolfram Research (2025), FrobeniusDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/FrobeniusDecomposition.html.
CMS
Wolfram Language. 2025. "FrobeniusDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrobeniusDecomposition.html.
APA
Wolfram Language. (2025). FrobeniusDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrobeniusDecomposition.html