CompanionMatrix[cvec]
returns a companion matrix corresponding to the coefficient vector cvec.
CompanionMatrix[{poly,x}]
returns a companion matrix corresponding to the polynomial poly in x.
CompanionMatrix[c,dir]
returns a companion matrix oriented by specification dir.


CompanionMatrix
CompanionMatrix[cvec]
returns a companion matrix corresponding to the coefficient vector cvec.
CompanionMatrix[{poly,x}]
returns a companion matrix corresponding to the polynomial poly in x.
CompanionMatrix[c,dir]
returns a companion matrix oriented by specification dir.
Details and Options


- Companion matrices provide the building blocks for the Frobenius decomposition of a matrix.
- CompanionMatrix[c] by default returns a matrix with subdiagonal elements equal to 1 and a last column that is comprised of the negated coefficients of the monic characteristic polynomial.
-
C=

- CharacteristicPolynomial[CompanionMatrix[C],x], up to sign, is
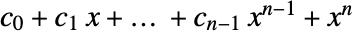 . MatrixMinimalPolynomial[CompanionMatrix[C],x] is exactly that polynomial. »
. MatrixMinimalPolynomial[CompanionMatrix[C],x] is exactly that polynomial. » - The companion matrix
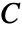 occurs naturally for cyclic subspaces: »
occurs naturally for cyclic subspaces: » 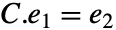 , …,
, …, 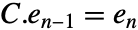 ,
, 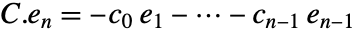
- where
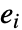 is UnitVector[n,i]. FrobeniusDecomposition returns a block companion matrix of this form.
is UnitVector[n,i]. FrobeniusDecomposition returns a block companion matrix of this form. - The transposed companion matrix occurs naturally when translating a single differential equation
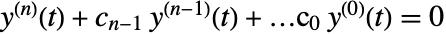 to state-space form using the states
to state-space form using the states 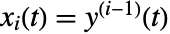 :
:
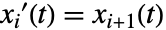 for
for  and
and 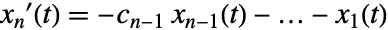 ⟹
⟹ ![x^(')(t)=TemplateBox[{C}, Transpose].x(t) x^(')(t)=TemplateBox[{C}, Transpose].x(t)](Files/CompanionMatrix.en/13.png) .
. - StateSpaceModel[TransferFunctionModel[…]] returns a system of this form.
- CompanionMatrix[cvec] assumes an implicit monic term of degree equal to the length of the list. Specifically, it treats the list cvec={c0,c1,…,cn-1} as coefficients to the polynomial
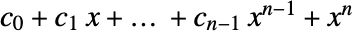 . »
. » - CompanionMatrix[{poly,x}] does not assume an implicit highest degree term. It does require that poly be explicitly a polynomial in x (of positive degree).
- CompanionMatrix[c,dir] uses dir to determine the resulting matrix layout. It must be one of Right (the default), Bottom, Left or Top. The coefficients for c will be placed using this directive.
- For Right or Left, the coefficients run down the last or first column, respectively, while for Bottom or Top, they run down the last or first row, respectively. For Right and Bottom, the coefficient of the constant term is first, while for Left and Top, the highest-degree term comes first. The band of ones will lie on the subdiagonal for Right and Top and on the superdiagonal for Bottom and Left.
- The most commonly used directions, Right and Bottom, are transposes of one another. Likewise, Top and Left are transposes of one another. »
- The eigenvalues of a companion matrix are the roots of poly, irrespective of the choice of orientation. »
- The following options can be given:
-
TargetStructure Automatic the structure of the returned matrix - Possible settings for TargetStructure include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Sparse" represent the matrix as a sparse array

Examples
open all close allBasic Examples (1)
Scope (3)
CompanionMatrix takes explicit polynomials:
CompanionMatrix takes symbolic input:
Give a list of coefficients and show its corresponding companion matrix:
CompanionMatrix uses a Right specification by default:
Instead locate the coefficients in the bottom row:
Check that these are transposes:
Locate the coefficients in the top row:
Locate the coefficients in the leftmost column:
Options (1)
TargetStructure (1)
By default, CompanionMatrix returns a dense matrix:
Instead return a SparseArray:
Properties & Relations (6)
CompanionMatrix[{a0+a1x+…+an-1 xn-1+xn,x}] and CompanionMatrix[{a0,…,an-1}] are the same:
For ![]() , MatrixMinimalPolynomial[CompanionMatrix[c],x] is
, MatrixMinimalPolynomial[CompanionMatrix[c],x] is ![]() 's associated polynomial
's associated polynomial ![]() :
:
Then CharacteristicPolynomial[c,x] is ![]() times the minimal polynomial:
times the minimal polynomial:
Compute the eigenvalues of a companion matrix:
These are the same as the roots of the corresponding polynomial:
All four possible layouts have the same eigenvalues:
The determinant of CompanionMatrix[{c0,c1,…}] is c0:
Equivalently, it is the constant term in the associated polynomial ![]() :
:
As a consequence, the matrix is invertible as long as ![]() :
:
Compute a characteristic polynomial of a matrix:
Build the companion matrix corresponding to that polynomial:
This agrees with the Frobenius normal form:
For c==CompanionMatrix[[c0,c1,…}], the vectors ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() are the standard basis for
are the standard basis for ![]() :
:
Possible Issues (1)
A coefficient list of two elements where the second is symbolic will be interpreted as a polynomial with the second element in the list being the variable:
Instead obtain the companion matrix of the polynomial with constant and linear terms corresponding to 3+x and x, respectively, and monic quadratic term:
Related Guides
History
Text
Wolfram Research (2025), CompanionMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/CompanionMatrix.html.
CMS
Wolfram Language. 2025. "CompanionMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompanionMatrix.html.
APA
Wolfram Language. (2025). CompanionMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompanionMatrix.html
BibTeX
@misc{reference.wolfram_2025_companionmatrix, author="Wolfram Research", title="{CompanionMatrix}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/CompanionMatrix.html}", note=[Accessed: 16-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_companionmatrix, organization={Wolfram Research}, title={CompanionMatrix}, year={2025}, url={https://reference.wolfram.com/language/ref/CompanionMatrix.html}, note=[Accessed: 16-January-2026]}