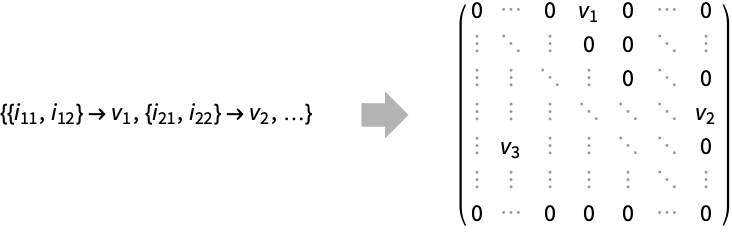
SparseArray[{pos1v1,pos2v2,…}]
yields a sparse array with all elements zero except for values vi at positions posi.
SparseArray[list]
yields a sparse array version of list.
SparseArray[data,{d1,d2,…}]
yields a sparse array representing a d1×d2×… array.
SparseArray[data,dims,val]
yields a sparse array in which unspecified elements are taken to have value val.


SparseArray
SparseArray[{pos1v1,pos2v2,…}]
yields a sparse array with all elements zero except for values vi at positions posi.
SparseArray[list]
yields a sparse array version of list.
SparseArray[data,{d1,d2,…}]
yields a sparse array representing a d1×d2×… array.
SparseArray[data,dims,val]
yields a sparse array in which unspecified elements are taken to have value val.
Details



- SparseArray is also known as sparse matrix.
- Sparse arrays are typically used for efficient linear algebra where most of the entries are zero and for graph adjacency matrices.
- A sparse array stores only the positions where there are nonzero values, but represents the full array:
- The data can have the following forms:
-
rules rules specifying positions and values. list convert an array to SparseArray SymmetrizedArray[…] convert to SparseArray QuantityArray[…] convert to SparseArray of Quantity SparseArray[…] minimize the explicit nonzero elements - With s=SparseArray[rules,…] the following specifications can be used:
-
{{i1 1,…,i1 r}v1,{i2 1,…,i2 r}v2,…} s[[i1 1, …, i1 r]] has value v1, s[[i2 1, …, i2 r]] has value v2, etc. pattv {{i1 1,…,i1 r}v,{i2 1,…,i2 r}v,…} for all {ik 1,…,ik r} that matches the pattern patt patt:>v evaluate the value v for each matching position Band[…]vals specify values for bands and subblocks {pos1,pos2,…}{v1,v2,…} equivalent to {pos1v1,pos2v2,…} - SparseArray conversions include:
-
Normal[SparseArray[…]] convert to the ordinary List array. SymmetrizedArray[SparseArray[…]] convert to a symmetrized array. ArrayRules[SparseArray[…]] give the list of rules {pos1->v1,pos2->v2,…} - A SparseArray object is a representation of an ordinary array, so many functions work like they would on the ordinary array. Examples include functions like Dimensions, Part, Plus and LinearSolve.
- SparseArray[data,…] is always converted to an optimized standard form with structure SparseArray[Automatic,dims,val,…].
- SparseArray is treated as a raw object by functions like AtomQ and for purposes of pattern matching.
- By default, SparseArray takes unspecified elements val to be zero.
- The elements in SparseArray need not be numeric, but cannot themselves be lists.
- SparseArray[…][prop] gives the property prop of the SparseArray object. The following properties may be given:
-
"ImplicitValue" gives the value for elements that are not given explicitly "ExplicitLength" gives the number of explicit values "ExplicitValues" gives the list of explicit values "ExplicitPositions" gives the list of positions corresponding to the explicit values "ColumnIndices" gives the column indices from the compressed sparse row representation "RowPointers" gives the row pointer list from the compressed sparse row representation "BandWidth" gives the off-diagonal bandwidth for a sparse matrix "Density" gives the ratio of the number of explicit elements to the total number of elements
Examples
open all close allBasic Examples (1)
Scope (7)
Make a large sparse depth-3 array:
Construct a tridiagonal matrix using patterns for indices:
Construct a 10,000×10,000 version:
Make a sparse diagonal matrix:
This is equivalent to DiagonalMatrix:
Except that as a sparse matrix, it uses much less memory:
Construct a block diagonal matrix using rules with Band:
Convert an ordinary matrix into a sparse matrix:
Make a rank-4 sparse tensor with values at random positions:
ArrayRules produces the minimal list of rules needed to specify the SparseArray:
Many typical operations work with SparseArray objects as they would for equivalent lists:
Arithmetic works elementwise just as it does for lists:
Matrix products are done with Dot:
Many linear algebra functions are done efficiently with the sparse form:
Generalizations & Extensions (2)
The unspecified elements can have any value:
Construct a sparse matrix with all machine-number values:
Construct a sparse matrix with exact integer values:
N[s] is the same as ns:
Applications (4)
Properties & Relations (3)
A SparseArray object is Equal to the corresponding ordinary list:
They are not SameQ because the expression structure is different:
For functions f that work with SparseArray objects, typically f[s]==f[Normal[s]]:
This includes all functions with the attribute Listable:
Convert linear expressions to SparseArray objects using CoefficientArrays:
Convert from SparseArray to expressions using Dot:
Possible Issues (9)
If a position is repeated in the rule list for SparseArray, the first instance is used:
SparseArray objects can represent data too large to represent in normal form:
Using Normal will give a SystemException:
Sparse operations do not by default check for cancellation:
Use SparseArray to recompute the sparse structure:
The internal structure of a SparseArray representation is not unique and SameQ detects this:
Use SparseArray to recompute the sparse structure:
Note that Equal works as expected:
The internal structure of SparseArray representation is not unique and setting parts can change that structure:
Test if the SparseArray instances are the same:
Use SparseArray to recompute the sparse structure:
Note that Equal works as expected:
Operations with side effects may give different values when iterating over SparseArray:
With Reap and Sow you can see what elements are accessed:
For a SparseArray object, Part gives parts of the represented list:
The FullForm is a way of reconstructing the object from basic storage information:
A SparseArray object is treated as atomic for functions that do not work on the representation:
Cases does not work on the represented matrix:
You can often use the result of ArrayRules to get the information without expanding:
Even for a dense SparseArray there can be a division by 0:
The density of a SparseArray is 1:
Since a density 1. SparseArray is a very special case, making this work would be computationally excessively expansive. In this case, the use of Normal is justified as the matrix is dense:
See Also
ArrayRules SparseArrayQ Normal Band CoefficientArrays ArrayPlot Array ConstantArray NumericArray Association
Function Repository: SparseAssociation
Related Guides
Related Workflows
- Create a Matrix
History
Introduced in 2003 (5.0) | Updated in 2007 (6.0) ▪ 2021 (13.0)
Text
Wolfram Research (2003), SparseArray, Wolfram Language function, https://reference.wolfram.com/language/ref/SparseArray.html (updated 2021).
CMS
Wolfram Language. 2003. "SparseArray." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/SparseArray.html.
APA
Wolfram Language. (2003). SparseArray. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SparseArray.html
BibTeX
@misc{reference.wolfram_2025_sparsearray, author="Wolfram Research", title="{SparseArray}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/SparseArray.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_sparsearray, organization={Wolfram Research}, title={SparseArray}, year={2021}, url={https://reference.wolfram.com/language/ref/SparseArray.html}, note=[Accessed: 17-January-2026]}