body& or Function[body]
is a pure (or "anonymous") function. The formal parameters are # (or #1), #2, etc.
x|->body or xbody or Function[x,body]
is a pure function with a single formal parameter x.
{x1,x2,…}|->body or {x1,x2,…}body or Function[{x1,x2,…},body]
is a pure function with a list of formal parameters.
Function[params,body,attrs]
is a pure function that is treated as having attributes attrs for purposes of evaluation.


Function 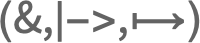
body& or Function[body]
is a pure (or "anonymous") function. The formal parameters are # (or #1), #2, etc.
x|->body or xbody or Function[x,body]
is a pure function with a single formal parameter x.
{x1,x2,…}|->body or {x1,x2,…}body or Function[{x1,x2,…},body]
is a pure function with a list of formal parameters.
Function[params,body,attrs]
is a pure function that is treated as having attributes attrs for purposes of evaluation.
Details

- When Function[body] or body& is applied to a set of arguments, # (or #1) is replaced by the first argument, #2 by the second, and so on. #0 is replaced by the function itself.
- If there are more arguments supplied than # i in the function, the remaining arguments are ignored. »
- ## stands for the sequence of all arguments supplied. »
- ## n stands for arguments from number n onward. »
- When applied to an association, #name is equivalent to #["name"], and picks out elements in the association.
- In the form #name, the characters in name can be any combination of alphanumeric characters not beginning with digits.
- The character is entered as
 |->
|-> ,
,  fn
fn or \[Function].
or \[Function]. - Function is analogous to λ in LISP or formal logic.
- Function has attribute HoldAll. The function body is evaluated only after the formal parameters have been replaced by arguments.
- The named formal parameters xi in Function[{x1,…},body] are treated as local, and are renamed xi$ when necessary to avoid confusion with actual arguments supplied to the function. »
- Function constructs can be nested in any way. Each is treated as a scoping construct, with named inner variables being renamed if necessary. »
- In Function[params,body,attrs], attrs can be a single attribute or a list of attributes. »
- Function[Null,body,attrs] represents a function in which the parameters in body are given using # etc.
Examples
open all close allBasic Examples (4)
Scope (15)
Use a Pure Function as an Argument (5)
Use a Pure Function as an Option Value (3)
Specify a custom comparison function in FixedPoint:
Return a Pure Function as a Result (4)
Derivative of a pure function:
Derivative of Tan:
Solutions of differential equations may be expressed as pure functions:
Generalizations & Extensions (4)
## n stands for arguments n and onward:
Create a pure function with attribute Listable:
Applications (3)
Properties & Relations (11)
#1 uses only the first argument supplied; the rest are ignored:
Not using any arguments results in a constant pure function:
Replacements can be done inside pure functions:
Formal parameters are renamed whenever there is a possibility of confusion:
The names of the parameters do not matter:
However, reusing a name introduces a new scope:
Nested functions take their arguments one at a time:
f[#]& is the same as simply f in the univariate case:
In general, f[##]& is the same as f:
Turn a formula involving a variable ![]() into a pure function:
into a pure function:
Use a formula in Table:
Use the corresponding pure function in an equivalent Array expression:
Special-purpose function constructs include InterpolatingFunction:
Possible Issues (4)
& binds more loosely than ->, so it usually needs parentheses in rules:
& binds more loosely than ?, so it usually needs parentheses in pattern tests:
Function does not evaluate its body until the function is applied:
Supplying fewer than the required number of arguments generates an error:
Neat Examples (2)
Define the recursion operator of recursion theory [more info]:
See Also
Apply Construct CurryApplied ApplyTo CompiledFunction InterpolatingFunction Slot SlotSequence FunctionCompile IncrementalFunction
Characters: \[Function]
Function Repository: ExpressionToFunction
Related Workflows
- Apply a Function to Cells in a Notebook
History
Introduced in 1988 (1.0) | Updated in 2008 (7.0) ▪ 2014 (10.0) ▪ 2020 (12.2)
Text
Wolfram Research (1988), Function, Wolfram Language function, https://reference.wolfram.com/language/ref/Function.html (updated 2020).
CMS
Wolfram Language. 1988. "Function." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Function.html.
APA
Wolfram Language. (1988). Function. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Function.html
BibTeX
@misc{reference.wolfram_2025_function, author="Wolfram Research", title="{Function}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Function.html}", note=[Accessed: 04-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_function, organization={Wolfram Research}, title={Function}, year={2020}, url={https://reference.wolfram.com/language/ref/Function.html}, note=[Accessed: 04-January-2026]}