CurryApplied[f,n]
represents an operator form of the function f of n arguments so that CurryApplied[f,n][x1]…[xn] is equivalent to f[x1,…,xn].
CurryApplied[n]
represents an operator form of CurryApplied that can be applied to a function to represent an operator form with n arguments.
CurryApplied[f,{i1,…,in}]
represents an operator form of the function f of n arguments so that CurryApplied[f,{i1,…,in}][x1]…[xn] is equivalent to f[xi1,…,xin].
CurryApplied[f,k{i1,…,in}]
represents an operator form that takes k arguments.


CurryApplied
CurryApplied[f,n]
represents an operator form of the function f of n arguments so that CurryApplied[f,n][x1]…[xn] is equivalent to f[x1,…,xn].
CurryApplied[n]
represents an operator form of CurryApplied that can be applied to a function to represent an operator form with n arguments.
CurryApplied[f,{i1,…,in}]
represents an operator form of the function f of n arguments so that CurryApplied[f,{i1,…,in}][x1]…[xn] is equivalent to f[xi1,…,xin].
CurryApplied[f,k{i1,…,in}]
represents an operator form that takes k arguments.
Details
- CurryApplied[f,arity][x1,…][y1,…]…[z1,…] is equivalent to CurryApplied[f,arity][x1,…,y1,…,z1,…], so that the structure of brackets is not relevant, only the number of arguments.
- CurryApplied[f,n] is equivalent to CurryApplied[f,{1,2,…,n}].
- CurryApplied[f,{i1,…,in}] is equivalent to CurryApplied[f,Max[{i1,…,in}]{i1,…,in}].
- CurryApplied[f,{i1,…,in,opts}][x1]…[xk] is equivalent to f[xi1,…,xin,opts] for a sequence opts of options.
- The ip
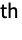 curried argument of CurryApplied[f,{i1,…,in}] will be the p
curried argument of CurryApplied[f,{i1,…,in}] will be the p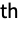 argument of f.
argument of f. - CurryApplied[arity][f] is equivalent to CurryApplied[f,arity].
Examples
open all close allBasic Examples (3)
Curry a function of two arguments:
Use the operator form of CurryApplied to do the same thing:
Curry a function of three arguments, keeping their order:
This is a curried form of Integrate that curries two integration variables:
Scope (7)
Curry the first argument of a function of two arguments:
Apply the function to any date object:
Curry the second argument of a function:
Curry a function of 3 arguments, keeping their order:
Curry a function of 3 arguments, applying a permutation before they are passed to the function:
These are curried operators taking 4 arguments, but only 2 of them are passed to the function f:
Use arguments of the curried function with any bracketing structure:
Curry Level with default option values:
Pass options to Level:
Applications (4)
Curry Composition of 3 functions:
Feed the 3 functions sequentially:
Apply the composition to an expression:
Specify how many arguments are functions to be composed:
Build an array of subscripted variables:
Build the K and S combinators using CurryApplied:
The combinations SKK and SKS are equivalent to the identity:
Properties & Relations (7)
CurryApplied[f,arity] represents the same operator as OperatorApplied[f,arity]:
CurryApplied[n][f] is equivalent to CurryApplied[f,n]:
OperatorApplied[f] is equivalent to OperatorApplied[f,{2,1}]:
For a function of zero arguments, CurryApplied[f,0] returns f[]:
If additional arguments are provided, the empty pair of brackets is still inserted:
Curry CurryApplied itself:
Compare to Construct:
For positive n, CurryApplied[Construct,n][f] is equivalent to CurryApplied[f,n-1]:
The relation also holds for n=1:
Compose two CurryApplied operators with a permutation and its inverse:
The result is equivalent to using CurryApplied without reordering the arguments:
Take two permutation lists of the same length:
Compose the corresponding CurryApplied operators:
Alternatively, use CurryApplied with their permutation product, in the same order:
Related Guides
History
Text
Wolfram Research (2020), CurryApplied, Wolfram Language function, https://reference.wolfram.com/language/ref/CurryApplied.html.
CMS
Wolfram Language. 2020. "CurryApplied." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CurryApplied.html.
APA
Wolfram Language. (2020). CurryApplied. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CurryApplied.html
BibTeX
@misc{reference.wolfram_2025_curryapplied, author="Wolfram Research", title="{CurryApplied}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CurryApplied.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_curryapplied, organization={Wolfram Research}, title={CurryApplied}, year={2020}, url={https://reference.wolfram.com/language/ref/CurryApplied.html}, note=[Accessed: 27-February-2026]}