Apply

f@@expr or Apply[f,expr]

replaces the head of expr by f.

Apply[f,expr,levelspec]

replaces heads in parts of expr specified by levelspec.

Apply[f]

represents an operator form of Apply that can be applied to an expression.

Details and Options

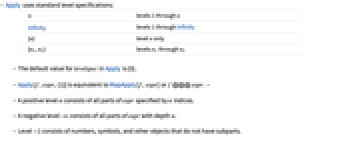
  • Apply uses standard level specifications:
  • nlevels 1 through n
    Infinitylevels 1 through Infinity
    {n}level n only
    {n1,n2}levels n1 through n2
  • The default value for levelspec in Apply is {0}.
  • Apply[f,expr,{1}] is equivalent to MapApply[f,expr] or f@@@expr. »
  • A positive level n consists of all parts of expr specified by n indices.
  • A negative level -n consists of all parts of expr with depth n.
  • Level -1 consists of numbers, symbols, and other objects that do not have subparts.
  • Level 0 corresponds to the whole expression.
  • With the option setting Heads->True, Apply will apply inside the heads of parts in addition to the parts themselves. »
  • Apply always effectively constructs a complete new expression and then evaluates it.
  • Apply operates on SparseArray objects and structured arrays just as it would on the corresponding ordinary lists. »
  • Apply on Association objects operates on values only. »
  • Apply[f][expr] is equivalent to Apply[f,expr].
  • Parallelize[Apply[f,expr,levelspec]] computes Apply[f,expr,levelspec] in parallel on all subkernels. »

Examples

open allclose all

Basic Examples  (6)

Replace the head of a list with f:

Equivalently:

Sum a list by replacing the head with Plus:

Apply gets rid of a level of lists:

Use the operator form of Apply:

Applying f to an Association keeps only values:

Applying a List to an Association is equivalent to Values:

Scope  (15)

Level Specifications  (10)

Apply at level 0 (default):

Apply at level 1:

Apply at levels 0 and 1:

Apply down to level 2 (excluding level 0):

Apply at levels 0 through 2:

Apply at all levels, starting at level 1:

Apply also at level 0:

Negative levels:

Positive and negative levels can be mixed:

Different heads at each level:

Apply also inside heads at the levels specified:

Types of Expressions  (5)

Apply works with any head, not just List:

Apply works on sparse arrays:

Use Apply with structured arrays, such as SymmetrizedArray:

Use Apply to apply a function to the rows of a structured array of type QuantityArray:

Apply f at the second level of an association; the association head is kept:

Apply f at several levels:

Options  (2)

Heads  (2)

Apply inside heads as well as arguments:

The option has no effect if including level zero:

Applications  (4)

Display the factorization of an integer using superscripts:

Create a table from a list of range specifications:

Turn a function that takes several arguments into one that takes a list of arguments:

Find random co-prime integers:

Properties & Relations  (5)

Total does effectively the same thing as applying Plus to a list:

Using ## in a pure function has the same effect as using Apply:

Three ways to apply a function at level 1:

Using Map:

Using MapApply:

Ordinary function application takes the list as a single argument:

Apply takes the elements of the list as separate arguments:

Compute Apply in parallel:

Possible Issues  (1)

Applying to atomic objects that do not have subparts effectively does nothing:

Wolfram Research (1988), Apply, Wolfram Language function, https://reference.wolfram.com/language/ref/Apply.html (updated 2014).

Text

Wolfram Research (1988), Apply, Wolfram Language function, https://reference.wolfram.com/language/ref/Apply.html (updated 2014).

CMS

Wolfram Language. 1988. "Apply." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Apply.html.

APA

Wolfram Language. (1988). Apply. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Apply.html

BibTeX

@misc{reference.wolfram_2025_apply, author="Wolfram Research", title="{Apply}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Apply.html}", note=[Accessed: 01-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_apply, organization={Wolfram Research}, title={Apply}, year={2014}, url={https://reference.wolfram.com/language/ref/Apply.html}, note=[Accessed: 01-July-2025 ]}