Total
Details and Options
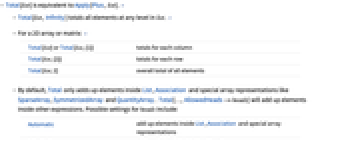
- Total[list] is equivalent to Apply[Plus,list]. »
- Total[list,Infinity] totals all elements at any level in list. »
- For a 2D array or matrix: »
-
Total[list] or Total[list,{1}] totals for each column Total[list,{2}] totals for each row Total[list,2] overall total of all elements - By default, Total only adds up elements inside List, Association and special array representations like SparseArray, SymmetrizedArray and QuantityArray. Total[…,AllowedHeads->heads] will add up elements inside other expressions. Possible settings for heads include:
-
Automatic add up elements inside List, Association and special array representations Inherited add up elements inside Head[expr] All add up elements inside any normal expression Association add up the values in Association List adds up elements in lists h add up elements inside h {h1,…} add up elements inside any of h1,… - Total[list,Method->"CompensatedSummation"] uses compensated summation to reduce numerical error in the result. »
- Total works with SparseArray objects. »
Examples
open all close allScope (6)
Use exact arithmetic to total the values:
Use 47-digit precision arithmetic:
Total the columns of a matrix:
Total by adding parts in the first dimension:
Total in the last dimension only:
Total in the last two dimensions:
Total all but the last dimension:
Total the last dimension in a ragged array:
You cannot total in the first dimension because the lists have incompatible lengths:
Options (2)
Method (1)
Use Method->"CompensatedSummation" to reduce accumulated errors in a sum:
Without compensated summation, small errors may accumulate with each term:
AllowedHeads (1)
Total[expr,AllowedHeads->Inherited] works with any head:
Applications (3)
Form a polynomial from monomials:
Show that the trace of a matrix is equal to the total of its eigenvalues:
Search for "perfect" numbers equal to the sum of their divisors:
Text
Wolfram Research (2003), Total, Wolfram Language function, https://reference.wolfram.com/language/ref/Total.html (updated 2019).
CMS
Wolfram Language. 2003. "Total." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Total.html.
APA
Wolfram Language. (2003). Total. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Total.html