



Sum 
Details and Options




- Sum[f,{i,imax}] can be entered as
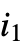 .
. 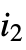 can be entered as
can be entered as 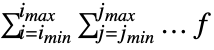 sum
sum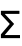 or \[Sum].
or \[Sum].- Sum[f,{i,imin,imax}] can be entered as
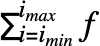 .
. - The limits should be underscripts and overscripts of
 in normal input, and subscripts and superscripts when embedded in other text.
in normal input, and subscripts and superscripts when embedded in other text. - Sum uses the standard Wolfram Language iteration specification.
- The iteration variable i is treated as local, effectively using Block.
- If the range of a sum is finite,
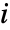 is typically assigned a sequence of values, with
is typically assigned a sequence of values, with 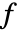 being evaluated for each one.
being evaluated for each one. - In multiple sums, the range of the outermost variable is given first. »
- The limits of summation need not be numbers. They can be Infinity or symbolic expressions. » »
- If a sum cannot be carried out explicitly by adding up a finite number of terms, Sum will attempt to find a symbolic result. In this case, f is first evaluated symbolically.
- The indefinite sum
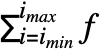 is defined so that its difference with respect to i gives f. »
is defined so that its difference with respect to i gives f. » - Definite and indefinite summation can be mixed in any order. »
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions False whether to generate conditions on parameters GeneratedParameters None how to name generated parameters Method Automatic method to use Regularization None what regularization scheme to use VerifyConvergence True whether to verify convergence - Possible values for Regularization include: None, "Abel", "Borel", "Cesaro", "Dirichlet", and "Euler". {reg1,reg2,…} specifies different schemes for different variables in a multiple sum.
- Method->"method" performs the summation using the specified method.
- Method->{"strategy",Method->{"meth1","meth2",…}} uses the methods "methi", controlled by the specified strategy method.
- Possible strategy methods include:
-
"SequentialFirstToSucceed" sequentially try each method until one succeeds "SequentialBestQuality" sequentially try each method and return the best result "ParallelFirstToSucceed" try each method in parallel until one succeeds "ParallelBestQuality" try each method in parallel and return the best result "IteratedSummation" use iterated univariate summation - Specific methods include:
-
Automatic automatically selected method "HypergeometricTermFinite" special finite hypergeometric term summation "HypergeometricTermGosper" indefinite hypergeometric term summation "HypergeometricTermPFQ" general definite hypergeometric term summation "HypergeometricTermZeilberger" definite hypergeometric term summation "LevelCounting" summation based on counting solutions in level sets "Logarithmic" logarithmic series summation "PeriodicFunction" periodic function summation "PolyGammaHypergeometricSeries" polygamma series representation summation "PolyGammaIntegralRepresentation" polygamma integral representation summation "PolyGammaSumByParts" polygamma summation by parts "Polynomial" polynomial summation "PolynomialExponential" polynomial exponential summation "PolynomialTrigonometric" polynomial trigonometric summation "Procedural" compute the sum procedurally "QHypergeometricTermGosper" indefinite q-hypergeometric term summation "QHypergeometricTermZeilberger" definite q-hypergeometric term summation "QRationalFunction" q-rational function summation "RationalExponential" rational times exponential summation "RationalFunction" rational function summation "RationalTrigonometric" rational trigonometric summation "TableLookup" summation based on table lookup - Sum can do essentially all sums that are given in standard books of tables.
- Sum is output in StandardForm using
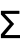 .
. - Parallelize[Sum[f,iter]] or ParallelSum[f,iter] computes Sum[f,iter] in parallel on all subkernels. »
Examples
open all close allBasic Examples (6)
Scope (45)
Basic Uses (11)
A definite sum over a finite range:
Using a finite list of elements:
Plot the sequence and its partial (or cumulative) sums:
A multiple sum over finite ranges:
Plot a multivariate sequence and its partial sums:
The outermost summation bounds can depend on inner variables:
Combine summation over lists with standard iteration ranges:
The elements in the iterator list can be any expression:
Multivariate sums over infinite ranges:
The difference is equivalent to the summand:
The definite sum is given as the difference of indefinite sums:
Multivariate indefinite summation:
Mixes of indefinite and definite summation:
Use GenerateConditions to get the conditions under which the answer is true:
Refine or simplify the resulting answer:
Use Assumptions to provide assumptions directly to Sum:
An infinite sum may not converge:
Some infinite sums can be given a finite value using Regularization:
Indefinite Sums (18)
Differences of expressions with a general function:
Polynomials can be summed in terms of polynomials:
Exponential sequences (geometric series):
The base-2 case plays the same role for sums as base- does for integrals:
Fibonacci and LucasL are exponential sequences with base GoldenRatio:
Exponential polynomials can be summed in terms of exponential polynomials:
Rational functions can be summed in terms of rational functions and PolyGamma:
Every difference of a rational function can be summed as a rational function:
In general, the answer will involve PolyGamma:
Every rational function can be summed:
Some rational exponential sums can be summed in terms of elementary functions:
In general, the answer involves special functions:
Every rational exponential function can be summed:
Trigonometric polynomials can be summed in terms of trigonometric functions:
Multiplied by an exponential and a polynomial:
Hypergeometric term sequences:
The DiscreteRatio is rational for all hypergeometric term sequences:
Many functions give hypergeometric terms:
Any products are hypergeometric terms:
Differences of hypergeometric terms can be summed as hypergeometric terms:
In general additional special functions are required:
Some ArcTan sums can be represented in terms of ArcTan:
Similarly for ArcCot sums:
Some trigonometric sums with exponential arguments have trigonometric representations:
Products of PolyGamma and other expressions:
HarmonicNumber and Zeta behave like PolyGamma sequences:
GammaRegularized sums:
BetaRegularized sums:
Multi-basic q-polynomial functions:
Mixed multi-basic q-polynomial functions:
In general QPolyGamma is needed to represent the solution:
Rational functions of hyperbolic functions can be reduced to q-rational sums:
Holonomic sequences generalize hypergeometric term sequences:
Any holonomic sequence can be summed:
Many special functions are holonomic:
Definite Sums (14)
Polynomials can be summed in terms of polynomials:
Polynomial exponentials can be summed in terms of polynomial exponentials:
Get the conditions for summability:
Rational functions can always be summed:
In general RootSum expressions are needed:
Some rational exponential functions can be summed as rational exponentials:
In general LerchPhi is required for the result:
The infinite sum is often simpler:
Trigonometric polynomials can be summed in terms of trigonometric functions:
Multiplied by a rational function:
Logarithms of polynomials and rational functions can always be summed:
In the infinite case there is also convergence analysis:
Get the conditions for convergence:
Some hypergeometric term sums can be summed in the same class:
In general HypergeometricPFQ functions are needed:
Products of PolyGamma and other expressions:
Combining with rational and rational exponential:
Products of Zeta and HarmonicNumber with other expressions:
These are typically called Euler sums:
GammaRegularized sums:
BetaRegularized sums:
ChebyshevU sums:
ChebyshevT sums:
StirlingS1 along columns, rows and diagonals multiplied by other expressions:
Similarly for StirlingS2:
Periodic sequences multiplied by other expressions:
Generalizations & Extensions (4)
Sum over the members of an arbitrary list:
ParallelSum computes Sum in parallel:
Sum can be parallelized automatically, effectively using ParallelSum:
Options (7)
Assumptions (1)
Use Assumptions to obtain a simpler answer for an indefinite logarithmic sum:
GenerateConditions (1)
GeneratedParameters (1)
Regularization (2)
By using Regularization, many sums can be given an interpretation:
Whenever a sum converges, the regularized value is the same:
Applications (8)
High School Algebra (1)
College Calculus (1)
Pascal's Triangle (1)
Study the properties of Pascal's triangle:
The sum of the numbers of any row in Pascal's triangle is a power of 2:
The alternating sum of the numbers in any row of Pascal's triangle is 0:
The sum of the squares of the numbers in the nth row of Pascal's triangle is Binomial[2n,n]:
Probability and Statistics (1)
Catalan Numbers (1)
Find the generating function for CatalanNumber:
Properties & Relations (10)
NSum will use numerical methods to compute sums:
Applying N to an unevaluated sum effectively uses NSum:
DifferenceDelta is the inverse operator for indefinite summation:
Sum effectively solves a special difference equation as solved by RSolve:
Several summation transforms are available including ZTransform:
ExponentialGeneratingFunction:
Sum uses SumConvergence to generate conditions for the convergence of infinite series:
Series computes a finite power series expansion:
SeriesCoefficient computes the ![]()
![]() power series coefficient:
power series coefficient:
FourierSeries computes a finite Fourier series expansion:
Total sums the entries in a list:
Accumulate generates the partial sums in a list:
Possible Issues (4)
Using Regularization may give a finite value:
The upper summation limit is assumed to be an integer distance from the lower limit:
Use GenerateConditions to get explicit assumptions:
This example gives an unexpected result above the threshold value of ![]() :
:
This happens due to symbolic evaluation of the first argument:
Force procedural summation to obtain the expected result:
Alternatively, prevent symbolic evaluation to avoid the incorrect result:
Sum gives an unexpected result for this example:
This happens due to symbolic evaluation of PrimeQ:
The sum returns unevaluated when it is expressed in terms of Primes:
Neat Examples (1)
Moments of Gaussian functions represented as EllipticTheta functions:
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2008 (7.0) ▪ 2019 (12.0)
Text
Wolfram Research (1988), Sum, Wolfram Language function, https://reference.wolfram.com/language/ref/Sum.html (updated 2019).
CMS
Wolfram Language. 1988. "Sum." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Sum.html.
APA
Wolfram Language. (1988). Sum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sum.html
BibTeX
@misc{reference.wolfram_2025_sum, author="Wolfram Research", title="{Sum}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Sum.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_sum, organization={Wolfram Research}, title={Sum}, year={2019}, url={https://reference.wolfram.com/language/ref/Sum.html}, note=[Accessed: 09-January-2026]}