



PolyGamma
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- PolyGamma[z] is the logarithmic derivative of the gamma function, given by
![TemplateBox[{z}, PolyGamma]=Gamma^'(z)/TemplateBox[{z}, Gamma] TemplateBox[{z}, PolyGamma]=Gamma^'(z)/TemplateBox[{z}, Gamma]](Files/PolyGamma.en/4.png) .
. - PolyGamma[n,z] is given for positive integer
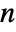 by
by ![TemplateBox[{n, z}, PolyGamma2]=d^nTemplateBox[{z}, PolyGamma]/dz^n TemplateBox[{n, z}, PolyGamma2]=d^nTemplateBox[{z}, PolyGamma]/dz^n](Files/PolyGamma.en/6.png) .
. - For arbitrary complex n, the polygamma function is defined by fractional calculus analytic continuation.
- PolyGamma[z] and PolyGamma[n,z] are meromorphic functions of z with no branch cut discontinuities.
- For certain special arguments, PolyGamma automatically evaluates to exact values.
- PolyGamma can be evaluated to arbitrary numerical precision.
- PolyGamma automatically threads over lists.
- PolyGamma can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (7)
Evaluate the digamma function:
Evaluate the pentagamma function:
Evaluate the second derivative of the gamma function:
Plot the digamma function over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (47)
Numerical Evaluation (7)
Evaluate for integer arguments of any size:
Evaluate for complex arguments and orders:
The precision of the output tracks the precision of the input:
Evaluate PolyGamma efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix PolyGamma function using MatrixFunction:
Specific Values (6)
Some singular points of PolyGamma:
Use FunctionExpand to expand higher-order polygamma functions:
Visualization (3)
Plot PolyGamma for half-integer values of parameter ![]() :
:
Function Properties (9)
Real domain of PolyGamma:
Approximate function ranges of PolyGamma for half-integer parameters:
PolyGamma is not an analytic function:
It has both singularities and discontinuities:
For fixed non-negative integer ![]() ,
, ![]() is a meromorphic function of
is a meromorphic function of ![]() :
:
It is not meromorphic for other values of ![]() :
:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
Differentiation (3)
First derivative of PolyGamma:
Integration (3)
Indefinite integral of PolyGamma:
Series Expansions (7)
Taylor expansion for the digamma function around ![]() :
:
Plot the first three approximations for the Euler gamma function around ![]() :
:
General term in the series expansion of the digamma function:
Series expansion at infinities:
Series expansion at a generic point:
Series expansion near a singularity:
PolyGamma can be applied to a power series:
Function Identities and Simplifications (5)
Use FullSimplify to simplify polygamma functions:
PolyGamma identity ![]() :
:
PolyGamma of a double argument:
Function Representations (4)
PolyGamma can be represented as a DifferenceRoot:
TraditionalForm formatting:
Applications (4)
Plot of the absolute value of PolyGamma over the complex plane:
The electric field energy of a charge at a fraction ![]() of the distance between parallel conducting plates:
of the distance between parallel conducting plates:
Final speed of a rocket with ![]() discrete propulsion events:
discrete propulsion events:
Final velocity in the limit of constant continuous propulsion:
Effective confining potential in random matrix theory for a Gaussian density of states:
Properties & Relations (7)
Use FullSimplify to simplify polygamma functions:
Express rational arguments through elementary functions:
Numerically find a root of a transcendental equation:
Generate PolyGamma from integrals, sums, and limits:
See Also
Gamma LogGamma EulerGamma HarmonicNumber QPolyGamma HurwitzZeta
Function Repository: PolyGammaSimplify
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1999 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2) ▪ 2007 (6.0) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1988), PolyGamma, Wolfram Language function, https://reference.wolfram.com/language/ref/PolyGamma.html (updated 2022).
CMS
Wolfram Language. 1988. "PolyGamma." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/PolyGamma.html.
APA
Wolfram Language. (1988). PolyGamma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolyGamma.html
BibTeX
@misc{reference.wolfram_2025_polygamma, author="Wolfram Research", title="{PolyGamma}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/PolyGamma.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_polygamma, organization={Wolfram Research}, title={PolyGamma}, year={2022}, url={https://reference.wolfram.com/language/ref/PolyGamma.html}, note=[Accessed: 05-March-2026]}