DifferenceRoot[lde][k]
gives the holonomic sequence ![]() , specified by the linear difference equation lde[h,k].
, specified by the linear difference equation lde[h,k].
DifferenceRoot[lde]
represents a pure holonomic sequence ![]() .
.


DifferenceRoot
DifferenceRoot[lde][k]
gives the holonomic sequence ![]() , specified by the linear difference equation lde[h,k].
, specified by the linear difference equation lde[h,k].
DifferenceRoot[lde]
represents a pure holonomic sequence ![]() .
.
Details

- Mathematical sequence, suitable for both symbolic and numerical manipulation; also known as holonomic sequence and P-recursive sequence.
- The holonomic sequence
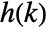 defined by a DifferenceRoot function satisfies a holonomic difference equation
defined by a DifferenceRoot function satisfies a holonomic difference equation 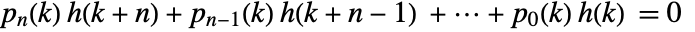 with polynomial coefficients
with polynomial coefficients 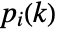 and initial values
and initial values 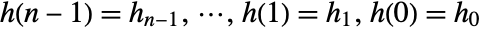 .
. - DifferenceRoot can be used like any other mathematical function.
- FunctionExpand will attempt to convert DifferenceRoot functions in terms of special functions.
- The sequences representable by DifferenceRoot include a large number of special sequences.
- DifferenceRootReduce can convert many special sequences to DifferenceRoot sequences.
- Holonomic sequences are closed under many operations, including:
-
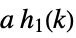 ,
, 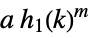
constant multiple, integer power 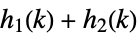 ,
, 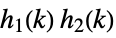
sums and products 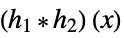
discrete convolution 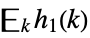 ,
, 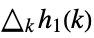 ,
, 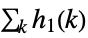
discrete shift, difference and sum - DifferenceRoot is automatically generated by functions such as Sum, RSolve and SeriesCoefficient.
- Functions such as Sum, DifferenceDelta and GeneratingFunction work with DifferenceRoot inputs.
- DifferenceRoot automatically threads over lists.
Examples
open all close allBasic Examples (2)
Define f to be the Fibonacci sequence:
Calculate the 20th Fibonacci number:
Compare the result with the built-in Fibonacci function:
Plot the first 10 Fibonacci numbers:
Calculate the sum of the first 30 Fibonacci numbers:
Find the generating function ![]() for the Fibonacci sequence:
for the Fibonacci sequence:
Find the first 10 coefficients of the series expansion of ![]() :
:
Compare the result with the first 10 Fibonacci numbers:
Several functions can produce closed-form answers by using DifferenceRoot functions:
Scope (21)
Numerical Evaluation (6)
Define a DifferenceRoot sequence:
Evaluate at an arbitrary point:
Evaluate sequences with inexact coefficients:
Evaluate sequences with complex coefficients:
Evaluate sequences with parameters:
Evaluate sequences for negative terms:
DifferenceRoot threads elementwise over lists and matrices:
Visualization (2)
Define a DifferenceRoot object called f:
Plot the first 25 terms of f using ListLinePlot:
Define a DifferenceRoot object f where the parameter a may be arbitrary:
Plot the sequence f for different values of the parameter a:
Function Properties (9)
DifferenceRoot works with linear recurrences:
DifferenceRoot transforms recurrences with rational coefficients to ones with polynomial coefficients:
Inhomogeneous recurrences are transformed to higher-order homogeneous recurrences:
DifferenceRoot works on inhomogeneous equations with polynomial forcing functions:
Calculate the first 10 terms of this sequence:
DifferenceRoot works with multiple initial values:
Difference function for a series with symbolic components:
Find the leading asymptotic term of a DifferenceRoot object as ![]() approaches Infinity:
approaches Infinity:
Obtain the same result using AsymptoticRSolveValue:
DifferenceRoot can take parameters:
Calculate the first 5 terms of this sequence for symbolic a:
Plot the sequence f for different values of the parameter a:
If possible, DifferenceRoot reduces to built-in functions:
Special Sequences (3)
Difference equation form of Fibonacci:
Difference equation form of LucasL:
Difference equation form of HarmonicNumber:
Differentiation (1)
Generate a parametric sequence corresponding to ChebyshevT polynomials:
Calculate the derivative of this sequence wrt to parameter:
Extract the difference equation that the derivatives of ChebyshevT obey:
Check the equality of the first 10 terms of this sequence with the direct derivatives of ChebyshevT:
Generalizations & Extensions (2)
Applications (6)
Use DifferenceRoot to get the difference equation form of HarmonicNumber:
Reduce combinations of special sequences to their DifferenceRoot forms:
Define the Pell number sequence using DifferenceRoot:
Prove properties of Pell numbers:
Reduce combinations of special sequences to a DifferenceRoot function:
Generate a function for which the Taylor expansion is the given DifferenceRoot object:
Generate the DifferenceRoot object that generates the BesselJ functions:
Properties & Relations (14)
Use DifferenceRootReduce to generate DifferenceRoot objects:
Get the corresponding ordinary difference equation:
Use the equation to verify solutions:
Sum of a DifferenceRoot object:
GeneratingFunction may generate a DifferentialRoot object from a holonomic sequence:
For specific cases, GeneratingFunction may give an explicit function:
Find the exponential generating function of a DifferenceRoot object:
The solution of a difference equation may be a DifferenceRoot object:
A result from Sum may be a DifferenceRoot object:
Coefficients in the expansion of a function may be given as a DifferenceRoot object:
The FindSequenceFunction result may be a DifferenceRoot object:
FunctionExpand attempts to generate simpler expressions for DifferenceRoot:
FunctionExpand attempts to generate simpler expressions for parametric sequences:
Define f to be some holonomic sequence:
Compare the result with the output of the RecurrenceTable:
DiscreteShift takes a DifferenceRoot function and generates a shifted sequence:
DifferenceDelta takes a DifferenceRoot function as an input:
Possible Issues (2)
DifferenceRoot evaluates only linear difference sequences with polynomial coefficients:
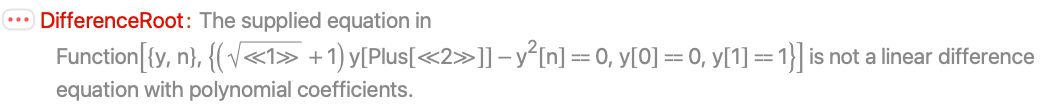
DifferenceRoot evaluates only integer terms:
Neat Examples (1)
Define a DifferenceRoot function:
See Also
DifferenceRootReduce DifferentialRoot RSolve RecurrenceTable LinearRecurrence FunctionExpand
Function Repository: FindLinearRecurrenceEquations
Tech Notes
Related Guides
Text
Wolfram Research (2008), DifferenceRoot, Wolfram Language function, https://reference.wolfram.com/language/ref/DifferenceRoot.html (updated 2020).
CMS
Wolfram Language. 2008. "DifferenceRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/DifferenceRoot.html.
APA
Wolfram Language. (2008). DifferenceRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferenceRoot.html
BibTeX
@misc{reference.wolfram_2025_differenceroot, author="Wolfram Research", title="{DifferenceRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DifferenceRoot.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_differenceroot, organization={Wolfram Research}, title={DifferenceRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/DifferenceRoot.html}, note=[Accessed: 23-January-2026]}