RecurrenceTable[eqns,expr,{n,nmax}]
generates a list of values of expr for successive n based on solving the recurrence equations eqns.
RecurrenceTable[eqns,expr,nspec]
generates a list of values of expr over the range of n values specified by nspec.
RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]
generates an array of values of expr for successive n1, n2, … .


RecurrenceTable
RecurrenceTable[eqns,expr,{n,nmax}]
generates a list of values of expr for successive n based on solving the recurrence equations eqns.
RecurrenceTable[eqns,expr,nspec]
generates a list of values of expr over the range of n values specified by nspec.
RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]
generates an array of values of expr for successive n1, n2, … .
Details and Options

- The eqns must be recurrence equations whose solutions over the range specified can be determined completely from the initial or boundary values given.
- The eqns can involve objects of the form a[n+i] where i is any fixed integer.
- The range specification nspec can have any of the forms used in Table.
- The following options can be given:
-
DependentVariables Automatic the list of all dependent variables Method Automatic method to use WorkingPrecision Automatic precision used in internal computations - With DependentVariables->Automatic, RecurrenceTable attempts to determine the dependent variables by analyzing the equations given.
- With WorkingPrecision->Automatic, results for exact inputs are computed exactly, and for inexact inputs, the precision to use is determined adaptively at each iteration.
- With WorkingPrecision->p, a fixed precision p is used for all iterations.
- RecurrenceTable[u[t]sys,resp,{t,tmin,tmax}] can be used for solving discrete-time models, where sys can be a TransferFunctionModel or a StateSpaceModel and the response function resp can be one of the following: »
-
"StateResponse" state response of sys to the input 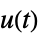
"OutputResponse" output response of sys to the input 
Examples
open all close allBasic Examples (4)
Scope (12)
Ordinary Difference Equations (6)
Linear ordinary difference equation with exact coefficients:
Nonlinear ordinary difference equation with inexact coefficients:
System of ordinary difference equation with symbolic initial conditions:
Iterate using exact arithmetic:
Iterate using adaptive arithmetic starting with precision 20:
The precision decreases with each iteration:
Iterate using fixed 20-digit-precision arithmetic:
Iterate using machine arithmetic:
Iterate several values at once by giving a vector initial condition:
Partial Difference Equations (2)
Difference-Algebraic Equations (1)
Solve a linear difference-algebraic equation with constant coefficients:
Compare with the symbolic solution given by RSolve:
Generalizations & Extensions (3)
Options (3)
DependentVariables (1)
Use DependentVariables to specify the variables when you only want to save some of them:
Method (1)
WorkingPrecision (1)
Use WorkingPrecision->MachinePrecision for the fastest iterations:
Use WorkingPrecision->p for slower, but higher-precision iterations:
Exact computations have no error, but may be very slow indeed:
Applications (6)
Logistic Equations (1)
Random Number Generation (1)
Rabbit Fractal (1)
Plot the Douady rabbit fractal:
Initial condition with 250 points in each direction on the rectangle with corners ![]() and
and ![]() :
:
Iterate starting from these initial conditions:
Use ArrayPlot to show the fractal:
Bifurcation Diagram of the Logistic Map (1)
Find iterates from ![]() and
and ![]() of the map
of the map ![]() for 1000 values of
for 1000 values of ![]() :
:
Scale the iterates to be integers between 1 and ![]() and transpose so the rows correspond to
and transpose so the rows correspond to ![]() :
:
Define a function that gives a rule based on the logarithm of counts of each value:
Make a sparse matrix based on applying Count to the iterates for each ![]() :
:
Use ArrayPlot to make the bifurcation diagram:
Compare Numerical Methods for ODEs (1)
For ![]() , Euler's method is unconditionally unstable:
, Euler's method is unconditionally unstable:
The symplectic Euler method is stable, but is very sensitive to initial conditions for large h:
Compare the methods for different vector fields with Manipulate:
Standard Map (1)
Stretching and folding induced by the standard map for a line of initial conditions [more info]:
Properties & Relations (3)
RSolve finds a symbolic solution for this difference equation:
RecurrenceTable generates a procedural solution for the same problem:
Use RecurrenceFilter to filter a signal:
Obtain the same result using RecurrenceTable:
Use RFixedPoints to find fixed points of a nonlinear recurrence equation:
Use RStabilityConditions to analyze the stability of the fixed points:
Solve the equation using RecurrenceTable:
Related Guides
Related Links
Text
Wolfram Research (2008), RecurrenceTable, Wolfram Language function, https://reference.wolfram.com/language/ref/RecurrenceTable.html (updated 2024).
CMS
Wolfram Language. 2008. "RecurrenceTable." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RecurrenceTable.html.
APA
Wolfram Language. (2008). RecurrenceTable. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RecurrenceTable.html
BibTeX
@misc{reference.wolfram_2025_recurrencetable, author="Wolfram Research", title="{RecurrenceTable}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RecurrenceTable.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_recurrencetable, organization={Wolfram Research}, title={RecurrenceTable}, year={2024}, url={https://reference.wolfram.com/language/ref/RecurrenceTable.html}, note=[Accessed: 12-March-2026]}