RSolve

RSolve[eqn,a[n],n]

solves a recurrence equation for a[n].

RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

solves a system of recurrence equations.

RSolve[eqn,a[n1,n2,…],{n1,n2,…}]

solves a partial recurrence equation.

Details and Options

  • RSolve[eqn,a,n] gives solutions for a as pure functions.
  • The equations can involve objects of the form a[n+λ] where λ is a constant, or in general, objects of the form a[ψ[n]], a[ψ[ψ[n]], a[ψ[…[ψ[n]]…]], where ψ can have forms such as:
  • n+λarithmetic difference equation
    μ ngeometric or 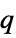-difference equation
    μ n+λarithmetic-geometric functional difference equation
    μ nαgeometric-power functional difference equation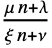
    linear fractional functional difference equation
  • Equations such as a[0]==val can be given to specify end conditions.
  • If not enough end conditions are specified, RSolve will give general solutions in which undetermined constants are introduced.
  • The specification a∈Vectors[m] or a∈Matrices[{m,p}] can be used to indicate that the dependent variable a is a vector-valued or a matrix-valued variable, respectively. Alternatively, a can be specified as a VectorSymbol or MatrixSymbol. » »
  • The constants introduced by RSolve are indexed by successive integers. The option GeneratedParameters specifies the function to apply to each index. The default is GeneratedParameters->C, which yields constants C[1], C[2], ….
  • GeneratedParameters->(Module[{C},C]&) guarantees that the constants of integration are unique, even across different invocations of RSolve.
  • For partial recurrence equations, RSolve generates arbitrary functions C[n][…].
  • Solutions given by RSolve sometimes include sums that cannot be carried out explicitly by Sum. Dummy variables with local names are used in such sums.
  • RSolve sometimes gives implicit solutions in terms of Solve.
  • RSolve handles both ordinary difference equations and ‐difference equations.
  • RSolve handles difference‐algebraic equations as well as ordinary difference equations.
  • RSolve can solve linear recurrence equations of any order with constant coefficients. It can also solve many linear equations up to second order with nonconstant coefficients, as well as many nonlinear equations.

Examples

open allclose all

Basic Examples  (4)

Solve a difference equation:

Include a boundary condition:

Get a "pure function" solution for a:

Substitute the solution into an expression:

Solve a functional equation:

Scope  (40)

Basic Uses  (7)

Compute the general solution of a first-order difference equation:

Obtain a particular solution by adding an initial condition:

Plot the solution of a first-order difference equation:

Make a table of values:

Verify the solution of a difference equation by using a in the second argument:

Obtain the general solution of a higher-order difference equation:

Particular solution:

Solve a system of difference equations:

Plot their solution:

Verify the solution:

Solve a partial difference equation:

Obtain a particular solution:

Plot the resulting solution:

Use different names for the arbitrary constants in the general solution:

Linear Difference Equations  (7)

Geometric equation:

First-order equation with variable coefficients:

A third-order constant coefficient equation:

Initial value conditions:

Plot the solution:

Second-order inhomogeneous equation:

Second-order variable coefficient equation in terms of elementary functions:

Euler–Cauchy equation:

In general, special functions are required to express solutions:

Higher-order inhomogeneous equation with constant coefficients:

Nonlinear Difference Equations  (5)

Solvable logistic equations:

Riccati equations:

Solutions in terms of trigonometric and hyperbolic functions:

Higher-order equations:

Nonlinear convolution equation:

Systems of Difference Equations  (8)

Linear system with constant coefficients:

With boundary conditions:

Plot their solution:

Linear fractional systems:

Diagonal system:

Variable coefficient linear system with a polynomial solution:

Linear constant coefficient difference-algebraic system:

An index-2 system:

Solve a linear system using vector variables:

Alternatively, define as a VectorSymbol:

Solve a linear system using matrix variables:

Alternatively, define as a MatrixSymbol:

Solve an inhomogeneous linear system of ODEs with constant coefficients:

Partial Difference Equations  (3)

First-order linear partial difference equation with constant coefficients:

Substitute the function Sin[2k] for the free function C[1]:

Plot the resulting solution:

Constant coefficient linear equation of orders 2, 3, and 4:

Inhomogeneous:

Variable coefficient linear equation:

Q–Difference Equations  (6)

First-order constant coefficient -difference equation:

Equivalent way of expressing the same equation:

Initial value:

Second-order equation:

Third-order:

Inhomogeneous:

Using a numeric value for :

Plot solution:

Linear varying coefficient equations:

Nonlinear equations:

Riccati equation:

A linear constant coefficient system of -difference equations:

Functional Difference Equations  (4)

Find the general solution for an arithmetic difference equation:

Verify the solution:

Solve an initial value problem for an arithmetic-geometric difference equation:

Plot the solution:

Solve a linear fractional difference equation:

Make a table of values for the solution:

Solve a geometric power difference equation:

Verify the solution:

Generalizations & Extensions  (1)

No boundary condition, gives two generated parameters:

One boundary condition:

Two boundary conditions:

Options  (1)

GeneratedParameters  (1)

Use differently named constants:

Use subscripted constants:

Applications  (11)

This models the amount a[n] at year n when the interest r is paid on the principal p only:

Here the interest is paid on the current amount a[n], i.e. compound interest:

Here a[n] denotes the number of moves required in the Tower of Hanoi problem with n disks:

Here a[n] is the number of ways to tile an n×3 space with 2×1 tiles:

The number of comparisons for a binary search problem:

Number of arithmetic operations in the fast Fourier transform:

The integral satisfies the difference equation:

The integral satisfies the difference equation:

The difference equation for the series coefficients of :

The determinant of an n×n tridiagonal matrix with diagonals satisfies:

This models the surface area s[n] in dimension n of a unit sphere:

The volume of the unit ball in dimension n:

Applying Newton's method to , or computing :

Applying the Euler forward method to yields:

Solve the difference equation that describes the complexity of Karatsuba multiplication:

Compare with the complexity of schoolbook multiplication:

Properties & Relations  (9)

Solutions satisfy their difference and boundary equations:

Difference equation corresponding to Sum:

Difference equation corresponding to Product:

RSolve returns a rule for the solution:

RSolveValue returns an expression for the solution:

RSolve finds a symbolic solution for a difference equation:

RecurrenceTable generates a procedural solution for the same problem:

FindLinearRecurrence finds the minimal linear recurrence for a list:

RSolve finds the sequence satisfying the recurrence:

Use RecurrenceFilter to filter a signal:

Solve the corresponding difference equation using RSolve:

Forecast the next value for a time series based on ARProcess:

Obtain the same result using RSolve:

Use RFixedPoints to find the fixed points for a system of two recurrence equations:

Use RStabilityConditions to analyze the stability of the fixed point:

Solve the system using a fixed point as the initial condition:

Solve the system for given initial conditions:

Plot the solution:

Possible Issues  (5)

Results may contain symbolic sums and products:

Capital and capital cannot be used as independent variables:

Replacing them by lowercase or lowercase fixes the issue:

The solution to this difference equation is unique as a sequence:

As a function it is only unique up to a function of period 1:

Boundary value problems may have multiple solutions:

Verify the solution when the equation involves subscripted variables:

Neat Examples  (1)

Compute the n^(th) iterate or composition of a function:

Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).

Text

Wolfram Research (2003), RSolve, Wolfram Language function, https://reference.wolfram.com/language/ref/RSolve.html (updated 2025).

CMS

Wolfram Language. 2003. "RSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/RSolve.html.

APA

Wolfram Language. (2003). RSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RSolve.html

BibTeX

@misc{reference.wolfram_2025_rsolve, author="Wolfram Research", title="{RSolve}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/RSolve.html}", note=[Accessed: 24-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_rsolve, organization={Wolfram Research}, title={RSolve}, year={2025}, url={https://reference.wolfram.com/language/ref/RSolve.html}, note=[Accessed: 24-May-2025 ]}