ARProcess

ARProcess[{a1,…,ap},v]

represents a weakly stationary autoregressive process of order p with normal white noise variance v.

ARProcess[{a1,…,ap},Σ]

represents a weakly stationary vector AR process with multinormal white noise covariance matrix Σ.

ARProcess[{a1,…,ap},v,init]

represents an AR process with initial data init.

ARProcess[c,…]

represents an AR process with a constant c.

Details

  • ARProcess is also known as AR or VAR (vector AR).
  • ARProcess is a discrete-time and continuous-state random process.
  • The AR process is described by the difference equation 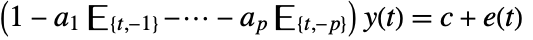, where 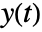is the state output, 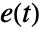is the white noise input, 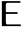is the shift operator, and the constant c is taken to be zero if not specified.
  • The initial data init can be given as a list {…,y[-2],y[-1]} or a single-path TemporalData object with time stamps understood as {…,-2,-1}.
  • A scalar AR process can have real coefficients ai and c, a positive variance v, and a non-negative integer order p.
  • An 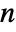-dimensional vector AR process can have real coefficient matrices ai of dimensions 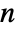×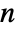, real vector c of length 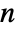, and the covariance matrix Σ should be symmetric positive definite of dimensions ×.
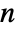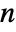  • The AR process with zero constant has transfer function 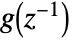, where:
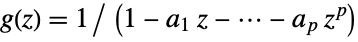
  • scalar process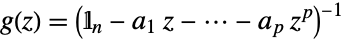
    vector process; 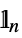is the 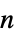× 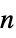identity matrix
  • ARProcess[tproc,p] for a time series process tproc gives an AR process of order p such that the series expansions about zero of the corresponding transfer functions agree up to degree p.
  • Possible time series processes tproc include ARProcess, ARMAProcess, and SARIMAProcess.
  • ARProcess[p] represents an autoregressive process of order p for use in EstimatedProcess and related functions.
  • ARProcess can be used with such functions as CovarianceFunction, RandomFunction, and TimeSeriesForecast.

Examples

open allclose all

Basic Examples  (3)

Simulate an AR process:

Covariance function:

Correlation function:

Partial correlation function:

Scope  (37)

Basic Uses  (11)

Simulate an ensemble of paths:

Simulate with given precision:

Simulate a first-order scalar process:

Sample paths for positive and negative values of the parameter:

Compare the serial dependence between consecutive values on scatter plots:

Simulate a weakly stationary process with given initial values:

For a process with a trend, initial values influence the behavior of the whole path:

Simulate a two-dimensional process:

Create a 2D sample path function from the data:

The color of the path is the function of time:

Create a 3D sample path function with time:

The color of the path is the function of time:

Simulate a three-dimensional process:

Create a sample path function from the data:

The color of the path is the function of time:

Estimate process parameters:

Compare the sample covariance functions with that of the estimated process:

Use TimeSeriesModel to automatically find orders:

Compare the sample covariance functions with the best time series model:

Find the maximum likelihood estimator:

Fix the constant and the variance and estimate the remaining parameters:

Plot the log-likelihood function together with the position of the estimated parameters:

Estimate a vector autoregressive process:

Compare covariance functions for each component:

Forecast future values:

Find the forecast for the next 10 steps:

Show the forecast path:

Plot the data and the forecasted values:

Find a forecast for a vector-valued time series process:

Find the forecast for the next 10 steps:

Plot the data and the forecast for each component:

Covariance and Spectrum  (6)

For low order it is possible to find the closed form of the correlation function:

Partial correlation function is zero for lags larger than the process order:

Correlation matrix:

Covariance matrix:

Inverse of the covariance matrix of an ARProcess is symmetric multidiagonal:

Covariance function for a vector-valued process:

Power spectral density:

Vector ARMAProcess:

Stationarity and Invertibility  (4)

Check if a time series process is weakly stationary:

For a vector process:

Find conditions for a process to be weakly stationary:

Find conditions for higher order:

Variance is positive only for a weakly stationary process:

Define stationarity conditions:

Variance is positive, assuming weak stationarity:

Autoregressive process is always invertible:

Estimation Methods  (6)

The available methods for estimating an ARProcess:

Compare log-likelihoods:

Method of moments admits the following solvers:

Use a general solver for moments when fixing or repeating parameters:

Maximum conditional likelihood method allows the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum likelihood method allows the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Spectral estimator allows specification of windows used for PowerSpectralDensity calculation:

Spectral estimator allows the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum entropy method:

It is also known as Burg method:

Process Slice Properties  (5)

Univariate SliceDistribution:

Multivariate slice distributions:

Slice distribution of a vector-valued time series:

First-order probability density function with zero initial conditions:

Stationary mean and variance:

Compare with the density function of a normal distribution:

Compute the expectation of an expression:

Calculate a probability:

Skewness and kurtosis functions are constant:

Moment:

Generating functions:

CentralMoment and its generating function:

FactorialMoment has no closed form for symbolic order:

Cumulant and its generating function:

Representations  (5)

Approximate an MA process with an AR process of order 3:

Compare the covariance function for the original and the approximate processes:

Approximate a vector process:

Approximate an ARMA process with an AR process:

Approximate an ARMA with fixed initial values:

Compare sample paths:

Approximate a SARIMA process with an AR process:

Compare sample paths:

TransferFunctionModel representation:

For a vector-valued process:

StateSpaceModel representation:

For a vector-valued process:

Applications  (6)

Use ARProcess to estimate an ARMAProcess:

Transform the estimated process to ARMA with given orders:

Compare log-likelihood values:

Consider the mean daily temperature for Champaign in August 2012:

Find process parameters:

Compare CorrelationFunction of the model and the data:

The hourly readings of temperature in June 2011 near your location:

Find model parameters:

Create TimeSeriesModel with estimated process:

Check goodness of fit by investigating residuals:

The daily exchange rates of the euro to the dollar from May 2012 through September 2012:

The scatter plot of consecutive values indicates strong serial correlation:

Fit an AR process to the exchange rates:

Forecast for 20 business days ahead:

Plot the forecast with original data:

Daily mean temperature readings in years 2000–2011 near your location:

Find process parameters:

Check stationarity assuming Automatic initial conditions:

Compare CorrelationFunction and PartialCorrelationFunction of the model and the sample:

The following data represents the return on DJIA and return on market capitalization for eight months during 1961. Fit a VAR model to this data:

Simulate the estimated process:

Find the mean path for each component:

Properties & Relations  (7)

ARProcess is a special case of an ARMAProcess:

ARProcess is a special case of an ARIMAProcess:

ARProcess is a special case of a FARIMAProcess:

ARProcess is a special case of a SARMAProcess:

ARProcess is a special case of a SARIMAProcess:

Squared values of an ARCHProcess follow an AR process:

CorrelationFunction and PartialCorrelationFunction of squared values:

The corresponding autoregressive process:

CorrelationFunction and PartialCorrelationFunction of the AR process:

Cumulated AR process is equivalent to an ARMAProcess:

Corresponding ARMA process:

Compare means:

Compare covariance functions:

Possible Issues  (5)

Some properties are defined only for wide-sense stationary processes:

Use FindInstance to find an example of a weakly stationary AR process:

A process without specified initial values must satisfy weak stationarity conditions:

Some properties will work after specifying initial value(s):

Add zero initial values:

Levinson–Durbin estimation method is not always applicable:

Use a different solver:

The method of moments may not find a solution in estimation:

Use a different solver:

Maximum entropy estimation method does not allow fixed or repeated parameters:

Use a different solver:

Neat Examples  (2)

Simulate a weakly stationary three-dimensional ARProcess:

Non-weakly stationary process, starting at the origin:

Simulate paths from an AR process:

Take a slice at 50 and visualize its distribution:

Plot paths and histogram distribution of the slice distribution at 50:

Wolfram Research (2012), ARProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ARProcess.html (updated 2014).

Text

Wolfram Research (2012), ARProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ARProcess.html (updated 2014).

CMS

Wolfram Language. 2012. "ARProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ARProcess.html.

APA

Wolfram Language. (2012). ARProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ARProcess.html

BibTeX

@misc{reference.wolfram_2024_arprocess, author="Wolfram Research", title="{ARProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ARProcess.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arprocess, organization={Wolfram Research}, title={ARProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ARProcess.html}, note=[Accessed: 30-December-2024 ]}