CovarianceFunction

CovarianceFunction[data,hspec]

estimates the covariance function at lags hspec from data.

CovarianceFunction[proc,hspec]

represents the covariance function at lags hspec for the random process proc.

CovarianceFunction[proc,s,t]

represents the covariance function at times s and t for the random process proc.

Details

  • CovarianceFunction is also known as autocovariance function.
  • The following specifications can be given for hspec:
  • τat time or lag τ
    {τmax}unit spaced from 0 to τmax
    {τmin,τmax}unit spaced from τmin to τmax
    {τmin,τmax,d τ}from τmin to τmax in steps of d τ
    {{τ1,τ2,…}}use explicit {τ1,τ2,…}
  • CovarianceFunction at lag h for data with mean 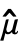and data values xi is given by:
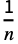
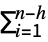  • (xi+h- 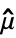)(xi-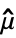)for scalar-valued data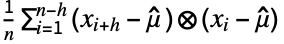
    1/(n)sum_(i=1)^(n-h)(x_(i+h)-mu^^ ) tensor (x_(i)-mu^^) for vector-valued data
  • When data is TemporalData containing an ensemble of paths, the output represents the average across all paths.
  • CovarianceFunction for a process proc with mean function μ[t] and value x[t] at time t is given by:
  • Expectation[(x[s]-μ[s])(x[t]-μ[t])]for a scalar-valued process
    Expectation[(x[s]-μ[s])⊗(x[t]-μ[t])]for a vector-valued process
  • The symbol ⊗ represents KroneckerProduct.
  • CovarianceFunction[proc,h] is defined only if proc is a weakly stationary process and is equivalent to CovarianceFunction[proc,h,0].
  • The process proc can be any random process, such as ARMAProcess and WienerProcess.

Examples

open allclose all

Basic Examples  (4)

Estimate the covariance function at lag 2:

The sample covariance function for a random sample from an autoregressive time series:

Calculate the covariance function for a discrete-time process:

Calculate the covariance function for a continuous-time process:

Scope  (13)

Empirical Estimates  (7)

Estimate the covariance function for some data at lag 9:

Obtain empirical estimates of the covariance function up to lag 9:

Compute the covariance function for lags 1 to 9 in steps of 2:

Compute the covariance function for a time series:

The covariance function of a time series for multiple lags is given as a time series:

Estimate the covariance function for an ensemble of paths:

Compare empirical and theoretical covariance functions:

Plot the cross-covariance for vector data:

Random Processes  (6)

The covariance function for a weakly stationary discrete-time process:

The covariance function only depends on the antidiagonal :

The covariance function for a weakly stationary continuous-time process:

The covariance function only depends on the antidiagonal :

The covariance function for a non-weakly stationary discrete-time process:

The covariance function depends on both time arguments:

The covariance function for a non-weakly stationary continuous-time process:

The covariance function depends on both time arguments:

The covariance function for some time-series processes:

Cross-covariance plots for a vector ARProcess:

Applications  (1)

Determine whether the following data is best modeled with an MAProcess or an ARProcess:

It is difficult to determine the underlying process from sample paths:

The covariance function of the data decays slowly:

ARProcess is clearly a better candidate model than MAProcess:

Properties & Relations  (14)

Sample covariance function is a biased estimator for the process covariance function:

Calculate the sample covariance function:

Covariance function for the process:

Plot both functions:

Covariance function for a process is the off-diagonal entry in the Covariance matrix:

Sample covariance function at lag 0 is a variance estimator:

Compare to the estimate using Variance:

The scaling factors are different:

Sample covariance function is related to CorrelationFunction:

Scaled sample correlation function:

Sample covariance function is related to AbsoluteCorrelationFunction:

Use Expectation to calculate the covariance function:

Covariance function for equal times reduces to Variance:

The covariance function is related to the AbsoluteCorrelationFunction :

For , the mean function is :

The covariance function is related to the Covariance:

It is the off-diagonal entry in the covariance matrix:

The covariance function is related to the CorrelationFunction :

For , the standard deviation function is :

Covariance function is invariant for ToInvertibleTimeSeries:

Covariance function is invariant to centralizing:

The data has nonzero mean:

Centralize data:

Compare covariance functions:

PowerSpectralDensity of a time series is a transform of the covariance function:

Use FourierSequenceTransform:

Compare to the power spectrum:

PowerSpectralDensity of data is a transform of the sample covariance function:

Apply ListFourierSequenceTransform:

Compare to SamplePowerSpectralDensity:

Possible Issues  (1)

CovarianceFunction output may contain DifferenceRoot:

Use FunctionExpand to recover explicit powers:

Wolfram Research (2012), CovarianceFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CovarianceFunction.html.

Text

Wolfram Research (2012), CovarianceFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/CovarianceFunction.html.

CMS

Wolfram Language. 2012. "CovarianceFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CovarianceFunction.html.

APA

Wolfram Language. (2012). CovarianceFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CovarianceFunction.html

BibTeX

@misc{reference.wolfram_2024_covariancefunction, author="Wolfram Research", title="{CovarianceFunction}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CovarianceFunction.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_covariancefunction, organization={Wolfram Research}, title={CovarianceFunction}, year={2012}, url={https://reference.wolfram.com/language/ref/CovarianceFunction.html}, note=[Accessed: 30-December-2024 ]}