Covariance[v,w]
gives the covariance between the vectors v and w.
Covariance[a,b]
gives the cross-covariance matrix for the matrices a and b.
Covariance[a]
gives the auto-covariance matrix for observations in matrix a.
Covariance[dist]
gives the auto-covariance matrix for the multivariate symbolic distribution dist.
Covariance[dist,i,j]
gives the (i,j)![]() covariance for the multivariate symbolic distribution dist.
covariance for the multivariate symbolic distribution dist.


Covariance
Covariance[v,w]
gives the covariance between the vectors v and w.
Covariance[a,b]
gives the cross-covariance matrix for the matrices a and b.
Covariance[a]
gives the auto-covariance matrix for observations in matrix a.
Covariance[dist]
gives the auto-covariance matrix for the multivariate symbolic distribution dist.
Covariance[dist,i,j]
gives the (i,j)![]() covariance for the multivariate symbolic distribution dist.
covariance for the multivariate symbolic distribution dist.
Details


- Covariance is typically used to measure covariation, i.e. whether one variable tends to vary similarly to another.
- Covariance[v,w] gives the unbiased estimate of the covariance
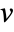 between v and w.
between v and w. - For vectors
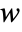 and
and 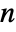 of length
of length 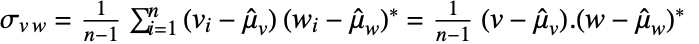 , the covariance estimate Covariance[v,w] is given by
, the covariance estimate Covariance[v,w] is given by 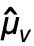 with
with  =Mean[v].
=Mean[v]. - For matrices
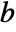 and
and 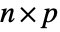 with dimensions
with dimensions 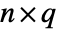 and
and 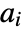 and columns indexed as
and columns indexed as 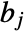 and
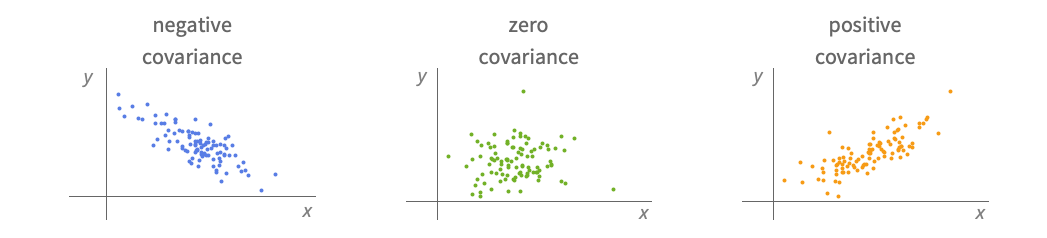
and 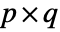 , respectively, Covariance[a,b] is a
, respectively, Covariance[a,b] is a 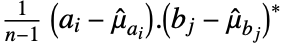 matrix with elements given by
matrix with elements given by 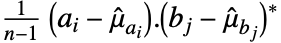 :
: - where
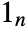 is an
is an 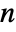 -vector of ones,
-vector of ones, 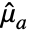 is Mean[a] and
is Mean[a] and 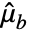 is Mean[b].
is Mean[b]. - For a matrix a with
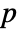 columns, Covariance[a] is a
columns, Covariance[a] is a 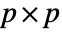 matrix given by Covariance[a, a].
matrix given by Covariance[a, a]. - Covariance works with any vector that is VectorQ or matrix that is MatrixQ.
- Covariance[dist,i,j] gives Expectation[(xi-μi)(xj-μj),{x1,x2,…}∈dist], where μi is the i
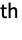 component of the mean of dist. »
component of the mean of dist. » - Covariance[dist] gives a covariance matrix with the (i,j)
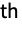 entry given by Covariance[dist,i,j]. »
entry given by Covariance[dist,i,j]. »
Examples
open all close allBasic Examples (3)
Scope (13)
Data (8)
Exact input yields exact output:
Approximate input yields approximate output:
Covariance between vectors of complexes:
A structured array can be used (see the guide):
Find the covariance for data involving quantities:
Distributions and Processes (5)
Covariance for a continuous multivariate distribution:
Covariance for a discrete multivariate distribution:
Covariance for derived distributions:
Covariance matrix for a random process at times s and t:
Covariance matrix for TemporalData at times ![]() and
and ![]() :
:
Applications (3)
Compute the covariance of two financial time series:
Covariance can be used to measure linear association:
Covariance can only detect monotonic relationships:
HoeffdingD can be used to detect a variety of dependence structures:
Properties & Relations (9)
The covariance matrix is symmetric and positive semidefinite:
A covariance matrix scaled by standard deviations is a correlation matrix:
Covariance and AbsoluteCorrelation are the same for a distribution with zero mean:
SpearmanRho is related to Covariance applied to ranks:
CovarianceFunction for a process is the off-diagonal entry in the covariance matrix:
Covariance and Correlation are the same for standardized vectors:
The covariance of a list with itself is the variance:
The diagonal of a covariance matrix is the variance:
The covariance tends to be large only on the diagonal of a random matrix:
See Also
Variance Correlation AbsoluteCorrelation CovarianceFunction CentralMoment Expectation PositiveSemidefiniteMatrixQ
Function Repository: TotalVariation WhiteningTransform
History
Introduced in 2007 (6.0) | Updated in 2010 (8.0) ▪ 2023 (13.3) ▪ 2024 (14.1)
Text
Wolfram Research (2007), Covariance, Wolfram Language function, https://reference.wolfram.com/language/ref/Covariance.html (updated 2024).
CMS
Wolfram Language. 2007. "Covariance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Covariance.html.
APA
Wolfram Language. (2007). Covariance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Covariance.html
BibTeX
@misc{reference.wolfram_2025_covariance, author="Wolfram Research", title="{Covariance}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Covariance.html}", note=[Accessed: 18-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_covariance, organization={Wolfram Research}, title={Covariance}, year={2024}, url={https://reference.wolfram.com/language/ref/Covariance.html}, note=[Accessed: 18-January-2026]}