Expectation[expr,xdist]
gives the expectation of expr under the assumption that x follows the probability distribution dist.
Expectation[expr,xdata]
gives the expectation of expr under the assumption that x follows the probability distribution given by data.
Expectation[expr,{x1,x2,…}dist]
gives the expectation of expr under the assumption that {x1,x2,…} follows the multivariate distribution dist.
Expectation[expr,{x1dist1,x2dist2,…}]
gives the expectation of expr under the assumption that x1, x2, … are independent and follow the distributions dist1, dist2, ….
Expectation[exprpred,…]
gives the conditional expectation of expr given pred.


Expectation
Expectation[expr,xdist]
gives the expectation of expr under the assumption that x follows the probability distribution dist.
Expectation[expr,xdata]
gives the expectation of expr under the assumption that x follows the probability distribution given by data.
Expectation[expr,{x1,x2,…}dist]
gives the expectation of expr under the assumption that {x1,x2,…} follows the multivariate distribution dist.
Expectation[expr,{x1dist1,x2dist2,…}]
gives the expectation of expr under the assumption that x1, x2, … are independent and follow the distributions dist1, dist2, ….
Expectation[exprpred,…]
gives the conditional expectation of expr given pred.
Details and Options

- Expectation is also known as expected value.
- xdist can be entered as x
 dist
dist dist or x \[Distributed]dist.
dist or x \[Distributed]dist. - exprpred can be entered as expr
 cond
cond pred or expr \[Conditioned]pred.
pred or expr \[Conditioned]pred. - For a continuous distribution dist, the expectation of expr is given by
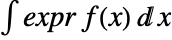 where
where 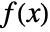 is the probability density function of dist and the integral is taken over the domain of dist.
is the probability density function of dist and the integral is taken over the domain of dist. - For a discrete distribution dist, the expectation of expr is given by
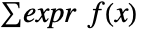 where
where 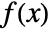 is the probability density function of dist and the summation is taken over the domain of dist.
is the probability density function of dist and the summation is taken over the domain of dist. - For a dataset data, the expectation of expr is given by Sum[expr,{x,data}]/Length[data].
- Univariate data is given as a list of values {v1,v2,…} and multivariate data is given as a list of vectors {{v11,…,v1m},{v21,…,v2m},…}.
- Expectation[expr,{x1dist1,x2dist2}] corresponds to Expectation[Expectation[expr,x2dist2],x1dist1] so that the last variable is summed or integrated first.
- N[Expectation[…]] calls NExpectation for expectations that cannot be done symbolically. »
- The following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters » GenerateConditions False whether to generate conditions on parameters Method Automatic what method to use » TargetUnits Automatic units to display in the output »
Background & Context
- Expectation[expr,x] gives the expectation for an expression expr involving a random variable x under the assumption that x either follows an indicated probability distribution (i.e. is a distribution such as NormalDistribution, BinomialDistribution, ChiSquareDistribution, etc.) or is taken from a given dataset (i.e. defines a dataset), and where is a shorthand for Distributed. The output of Expectation may be a number or symbolic expression involving the input parameters.
- Expectation also works with multivariate distributions, with nonparametric distributions such as EmpiricalDistribution, HistogramDistribution, and KernelMixtureDistribution, and with derived distributions such as TransformedDistribution and ProductDistribution. Expectation may also be applied to random processes, including those defined by ContinuousMarkovProcess, DiscreteMarkovProcess, WienerProcess, and PoissonProcess.
- Expressions passed to Expectation may include linear and nonlinear expressions as well as functions of both real and complex variables. Expectation can compute conditional expectations using an expression of the form exprpred, where is a shorthand for Conditioned. A number of options may be passed to Expectation including Assumptions, GenerateConditions, and Method. The output provided by Expectation is calculated via exact methods, including symbolic integration and summation. Corresponding results involving numerical methods can be obtained via NExpectation.
- By definition, the expectation Expectation[x,x] of a random variable x distributed according to a distribution is the same as the first moment Moment[,1] and hence also as the mean Mean[]. In addition, pairing Expectation with a Boole construct allows results obtained by Expectation to also be obtained by Probability. For example, Expectation[Boole[1<x<3],xNormalDistribution[]] is equivalent to Probability[1<x<3, xNormalDistribution[]].
Examples
open all close allBasic Examples (3)
Scope (31)
Basic Uses (9)
Compute the expectation for an expression in a continuous univariate distribution:
Discrete univariate distribution:
Continuous multivariate distribution:
Discrete multivariate distribution:
Find the expectation of an expression in a distribution specified by a list:
Compute the expectation using independently distributed random variables:
Find the conditional expectation with general nonzero probability conditioning:
Discrete univariate distribution:
Multivariate continuous distribution:
Multivariate discrete distribution:
Compute the conditional expectation with a zero-probability conditioning event:
Apply N[Expectation[…]] to invoke NExpectation if symbolic evaluation fails:
With no Assumptions, conditions are generated:
With Assumptions, a result valid under the given assumptions is returned:
Find the expectation of a rational function:
Compute an expectation for a time slice of a Poisson process:
Quantity Uses (5)
Find expectations of quantity expressions:
Find expectations specified using QuantityDistribution:
Find conditional expectations:
Calculate expectation with QuantityMagnitude:
Calculate expectation with distribution given by Quantity data:
Distribution given by QuantityArray:
Parametric Distributions (4)
Nonparametric Distributions (4)
Compute an expectation using a univariate EmpiricalDistribution:
Using a multivariate empirical distribution:
Using a univariate HistogramDistribution:
A multivariate histogram distribution:
Using a univariate KernelMixtureDistribution:
Using censored data with SurvivalDistribution:
Derived Distributions (9)
Compute the expectation using a TransformedDistribution:
An equivalent way of formulating the same expectation:
Find the expectation using a ProductDistribution:
An equivalent formulation for the same expectation:
Using a component mixture of normal distributions:
Parameter mixture of exponential distributions:
Truncated Dirichlet distribution:
Censored triangular distribution:
Generalizations & Extensions (2)
Options (6)
Assumptions (1)
With no Assumptions, conditions are generated:
With Assumptions, a result valid under the given assumptions is returned:
Method (4)
Compute the expectation of a polynomial function:
Obtain the same result using the moments of the distribution:
The evaluation is slower using the definition of Expectation as an integral:
Compute the expectation of a transcendental function:
Here, the method based on moments fails because the expression is nonpolynomial:
The result can be obtained using the definition of Expectation as a symbolic sum:
Find the expectation of a function in a TukeyLambdaDistribution:
The PDF of this distribution is not available in closed form:
Hence a direct application of the definition fails:
The expectation can be computed using Quantile:
Calculate the expectation of an expression:
This example uses Integrate:
Use Activate to evaluate the result:
TargetUnits (1)
Create a distribution object with quantity:
Expectation uses the quantity provided in the distribution as default:
Applications (20)
Distribution Properties (5)
Obtain the raw moments of a continuous distribution:
Obtain the mean of a discrete distribution:
Obtain the variance of a truncated distribution:
Construct a mixture density, here a Poisson‐inverse Gaussian mixture:
Obtain the same result directly using ParameterMixtureDistribution:
Verify Jensen inequality ![]() for a concave function
for a concave function ![]() and a lognormal distribution:
and a lognormal distribution:
Actuarial Science (5)
An insurance policy reimburses a loss up to a benefit limit of 10. The policy holder's loss ![]() follows a distribution with density function
follows a distribution with density function ![]() for
for ![]() and 0 otherwise. Find the expected value of the benefit paid under the insurance policy:
and 0 otherwise. Find the expected value of the benefit paid under the insurance policy:
An insurance company's monthly claims are modeled by a continuous, positive random variable ![]() , whose probability density function is proportional to
, whose probability density function is proportional to ![]() where
where ![]() . Determine the company's expected monthly claims:
. Determine the company's expected monthly claims:
Claim amounts for wind damage to insured homes are independent random variables with common density function ![]() for
for ![]() and 0 otherwise, where
and 0 otherwise, where ![]() is the amount of a claim in thousands. Suppose three such claims will be made. Find the expected value of the largest of the three claims:
is the amount of a claim in thousands. Suppose three such claims will be made. Find the expected value of the largest of the three claims:
Let ![]() represent the age of an insured automobile involved in an accident. Let
represent the age of an insured automobile involved in an accident. Let ![]() represent the length of time the owner has insured the automobile at the time of the accident.
represent the length of time the owner has insured the automobile at the time of the accident. ![]() and
and ![]() have joint probability density function
have joint probability density function ![]() for
for ![]() and
and ![]() , and 0 otherwise. Calculate the expected age of an insured automobile involved in an accident:
, and 0 otherwise. Calculate the expected age of an insured automobile involved in an accident:
Under an excess of loss reinsurance agreement, a claim is shared between the insurer and reinsurer only if the claim exceeds a fixed amount, called the retention level. Otherwise, the insurer pays the claim in full. Compute the expected value of the amounts ![]() and
and ![]() , paid by the insurer and the reinsurer for a retention level of
, paid by the insurer and the reinsurer for a retention level of ![]() if the claims follow a lognormal distribution with parameters
if the claims follow a lognormal distribution with parameters ![]() and
and ![]() . Find the expected insurer claim payouts:
. Find the expected insurer claim payouts:
Finance (2)
Compute the expected time value of a death benefit of $1 paid at time ![]() , where
, where ![]() is drawn from a Gompertz–Makeham distribution:
is drawn from a Gompertz–Makeham distribution:
Find the annual premium, which is usually paid at the beginning of a policy year, that is necessary to make the expected time value of that payment stream for ![]() periods (where
periods (where ![]() is drawn from a Gompertz–Makeham distribution) equal to the net single premium:
is drawn from a Gompertz–Makeham distribution) equal to the net single premium:
The resulting net annual premium:
The fractional change of stock price ![]() at time
at time ![]() (in years) is assumed lognormally distributed with parameters
(in years) is assumed lognormally distributed with parameters ![]() and
and ![]() :
:
Compute expected stock price at epoch ![]() :
:
Assuming an investor can invest money in a stock with dividend yield ![]() for a year at a continuously compounded yearly rate
for a year at a continuously compounded yearly rate ![]() risk-free, the risk-neutral pricing condition requires:
risk-free, the risk-neutral pricing condition requires:
Consider a call option to buy this stock a year from now, at a fixed price ![]() . The value of such an option is:
. The value of such an option is:
Similarly, consider a put option to sell this stock a year from now, at a fixed price ![]() . The value of such an option is:
. The value of such an option is:
The risk-neutral price of the call and put options are determined as the present value of their expected option values:
You can now establish the celebrated Put-Call Parity relationship that ![]() :
:
Assuming rate ![]() of 5%, dividend yield of 2%, volatility parameter
of 5%, dividend yield of 2%, volatility parameter ![]() of 0.087, an initial price of $200 per share of stock, and a strike price of $190 per share, the Black–Scholes call and put option prices are:
of 0.087, an initial price of $200 per share of stock, and a strike price of $190 per share, the Black–Scholes call and put option prices are:
The above results can be compared favorably with FinancialDerivative:
Risk and Reliability (2)
Random Experiments (2)
A random sample of size 10 from a continuous distribution ![]() is sorted in ascending order. A new random variate is generated. Find the probability that the 11
is sorted in ascending order. A new random variate is generated. Find the probability that the 11![]() sample falls between the fourth and fifth smallest values in the sorted list:
sample falls between the fourth and fifth smallest values in the sorted list:
The probability equals ![]() and is independent of
and is independent of ![]() :
:
It is also independent of the distribution:
Four six-sided dice are rolled. Find the expectation of the minimum value:
Find the expectation of the maximum value:
Find the expectation of the sum of the three largest values. Using the identity ![]() and linearity of Expectation, you get:
and linearity of Expectation, you get:
Other Applications (4)
A player bets amount ![]() in a casino with no betting limit in a game with a chance of winning
in a casino with no betting limit in a game with a chance of winning ![]() . If he loses he doubles the bet, and if he wins he quits, hence the number of games played follows a geometric distribution, with expected number of games played represented as follows:
. If he loses he doubles the bet, and if he wins he quits, hence the number of games played follows a geometric distribution, with expected number of games played represented as follows:
The cash reserve needed to win the ![]()
![]() game:
game:
The player always leaves the casino collecting the amount of the initial bet:
The cash reserve needed to execute the above strategy is finite only for strictly favorable games, where ![]() :
:
A drug has proven to be effective in 40% of cases. Find the expected number of successes when applied to 700 cases:
A baseball player is a 0.300 hitter. Find the expected number of hits if the player comes to bat 3 times:
Find the mean if the signal-to-noise ratio has a Weibull distribution:
Properties & Relations (10)
The expectation of an expression in a continuous distribution is defined by an integral:
The expectation of an expression in a discrete distribution is defined by a sum:
A conditional expectation is defined by a ratio of expectation and probability:
Use NExpectation to find the numerical value of an expectation:
Compute the probability of an event:
Obtain the same result using Expectation:
N[Expectation[…]] is equivalent to NExpectation if symbolic evaluation fails:
Use AsymptoticExpectation to find an asymptotic approximation of an expectation:
Obtain the same result using Asymptotic[Expectation[…]]:
Mean, Moment, Variance, and other properties are defined as expectations:
Generating functions including MomentGeneratingFunction are defined by an expectation:
For a distribution specified by a list, Expectation is equivalent to using Mean:
Possible Issues (1)
By default, the GenerateConditions for Integrate is set to False and Expectation may give the wrong result:
In fact, this expectation is undefined:
Set GenerateConditions to True to ensure the correct result:
Text
Wolfram Research (2010), Expectation, Wolfram Language function, https://reference.wolfram.com/language/ref/Expectation.html (updated 2016).
CMS
Wolfram Language. 2010. "Expectation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Expectation.html.
APA
Wolfram Language. (2010). Expectation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Expectation.html
BibTeX
@misc{reference.wolfram_2025_expectation, author="Wolfram Research", title="{Expectation}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/Expectation.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_expectation, organization={Wolfram Research}, title={Expectation}, year={2016}, url={https://reference.wolfram.com/language/ref/Expectation.html}, note=[Accessed: 23-January-2026]}