ProductDistribution[dist1,dist2,…]
represents the joint distribution with independent component distributions dist1, dist2, ….


ProductDistribution
ProductDistribution[dist1,dist2,…]
represents the joint distribution with independent component distributions dist1, dist2, ….
Details
- The probability density for ProductDistribution[dist1,dist2,…] is given by
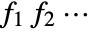 where
where 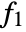 is the PDF of dist1,
is the PDF of dist1, 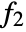 is the PDF of dist2, etc.
is the PDF of dist2, etc. - The notation {disti,n} indicates that disti is repeated n times.
- The distributions disti can be any combination of univariate, multivariate, continuous, or discrete distributions.
- ProductDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- ProductDistribution[dist1,dist2,…,distn] represents a multivariate statistical distribution whose
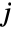
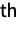 marginal distribution (MarginalDistribution) is precisely distj, and for which the component distributions dist1,dist2,…,distn are independent. In particular, the probability density function (PDF) of a general product distribution ProductDistribution[dist1,dist2,…,distn] is precisely
marginal distribution (MarginalDistribution) is precisely distj, and for which the component distributions dist1,dist2,…,distn are independent. In particular, the probability density function (PDF) of a general product distribution ProductDistribution[dist1,dist2,…,distn] is precisely 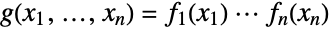 , where
, where 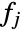 is the PDF of distj. While all product distributions share these properties, the characteristics and behavior of specific product distributions depend on their marginals dist1,dist2,…,distn.
is the PDF of distj. While all product distributions share these properties, the characteristics and behavior of specific product distributions depend on their marginals dist1,dist2,…,distn. - The component distributions dist1,dist2,…,distn may be continuous or discrete, univariate or multivariate, and may consist of any and all combinations of standard named distributions (e.g. BinomialDistribution, NormalDistribution, HypergeometricDistribution, etc.) and modifications (via TransformedDistribution, CensoredDistribution, ProductDistribution, CopulaDistribution, etc.) thereof. Moreover, each component distribution distj may be either symbolic (e.g. NormalDistribution[μ,σ]) or numeric (e.g. NormalDistribution[0,1]), and the shorthand ProductDistribution[{dist1,k1},{dist2,k2},… ,{distn,kn}] may be used to indicate that the j
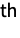 marginal distj is repeated kj times.
marginal distj is repeated kj times. - A program for beginning a systematic study of product distributions was proposed in the 1940s. Despite work throughout the 1950s and early 1960s toward that end, the first thorough treatment of the topic was a 1966 paper by Springer and Thompson. Since then, methods have been improved upon so that products of specially defined (e.g. piecewise) probability distributions can be studied both theoretically and algorithmically, and from a practical standpoint, product distributions have proven to be of tantamount importance in fields such as machine learning and finance. Product distributions have also been studied extensively using Monte Carlo theory and other numerical methods.
- Many relationships exist between ProductDistribution and various other distributions. ProductDistribution is a special case of CopulaDistribution in the sense that ProductDistribution[dist1,dist2,…,distn] is equivalent to CopulaDistribution["Product",{dist1,dist2,…,distn}]. KDistribution is defined to be a product of variates distributed according to GammaDistribution, the product of two instances of LogNormalDistribution is again LogNormalDistribution, and the product of BetaDistribution with GammaDistribution is again GammaDistribution. MultinormalDistribution (and hence BinormalDistribution) with a diagonal covariance matrix is also an example of ProductDistribution whose marginals are NormalDistribution.
Examples
open all close allBasic Examples (3)
Scope (26)
Basic Uses (7)
Define a product of two independent continuous distributions:
The PDF is the product of the component PDFs:
Product of discrete distributions:
The PDF is the product of the component PDFs:
Define a product distribution in which three components are repeated:
Probability density function for the four-dimensional product distribution:
Product distribution with both continuous and discrete components:
Draw a random sample from this distribution:
Estimate the distribution parameters for the components using the random sample:
Define a general product distribution with few repeated components:
Product of multivariate continuous distributions:
Verify that the integral of the PDF is 1:
Product of multivariate discrete distributions:
Parametric Distributions (6)
Create a bivariate normal distribution with independent components:
Compare to BinormalDistribution:
Define a two-dimensional Laplace distribution:
Define product distribution of independent PoissonDistribution:
The MultivariatePoissonDistribution does not have independent components:
Create the product distribution of two independent examples of StudentTDistribution:
Fit a MultivariateTDistribution:
Compute properties with symbolic parameters:
Moments with closed forms for symbolic order:
Other moments can be obtained numerically:
Find marginals of MultinormalDistribution:
Find product distribution of the marginal distributions:
Probability density function of :
is a MultinormalDistribution with a diagonal covariance matrix:
Nonparametric Distributions (3)
Define the product of SmoothKernelDistribution:
Compare to the product of original distributions:
Create a sample from and define SmoothKernelDistribution for this sample:
Compare all three distributions:
Define a product of EmpiricalDistribution:
Plot the probability density function and cumulative distribution function:
Define a product distribution with HistogramDistribution:
Derived Distributions (10)
Define a product with a CensoredDistribution:
MarginalDistribution chooses the components of ProductDistribution:
Compose product distribution from marginals:
It is the same as for binormal distribution with no correlation:
The components of product distribution are assumed to be independent, hence the original distribution cannot be recovered when ![]() is not zero:
is not zero:
Create the product distribution from a MixtureDistribution:
Find the product distribution of minimum and maximum OrderDistribution:
Plot density function for fixed ![]() :
:
Define a product distribution of a ParameterMixtureDistribution:
Product distribution is used as an input for a TransformedDistribution:
Find the product distribution of a TransformedDistribution:
Find the product distribution of a TruncatedDistribution:
Variance depends on the truncation interval:
Compare the PDF to the product of distributions that are not truncated:
Find the product distribution of a TruncatedDistribution:
Compare the PDF with the product distribution of two Poisson distributions:
Truncation influences the direction and value of skewness:
Product of QuantityDistribution evaluates to QuantityDistribution:
Applications (8)
Generate an uncorrelated sample from a binormal distribution:
The sample is slightly correlated, even though the original distribution is not:
Estimate the distribution from data:
The estimated distribution has correlation similar to the sample:
Force independent estimates by estimating the marginal distributions:
The resulting distribution has no correlation:
Two people try to meet at a certain place between 5pm and 5:30pm. Each person arrives at a time uniformly distributed in the time interval independently of each other and stays for five minutes. Find the probability that they meet:
Show the region for the overlapping event:
Two six-sided dice are thrown independently of each other. Find the density of the sum:
Find the density of the sum when three dice are thrown independently:
Find the probability that the values lie outside a circle of radius 7, in a square of side 14:
Generate random samples of size 100 from a standard normal distribution:
The sampling distribution for the mean is given by NormalDistribution[0,1/10]:
A lottery sells 10 tickets for $1 per ticket. Each time there is only one winning ticket. A gambler has $5 to spend. Find his probability of winning if he buys 5 tickets in 5 different lotteries:
His probability of winning is greater if he buys 5 tickets in the same lottery:
The waiting times for buying tickets and for buying popcorn at a movie theater are independent and they both follow the exponential distribution. The average waiting time for buying a ticket is 10 minutes and the average waiting time for buying popcorn is 5 minutes. Find the probability that a moviegoer waits for a total of less than 25 minutes before taking his or her seat:
Obtain the numerical value of the probability directly:
A factory produces cylindrically shaped roller bearings. The diameters of the bearings are normally distributed with mean 5 cm and standard deviation 0.01 cm. The lengths of the bearings are normally distributed with mean 7 cm and standard deviation 0.01 cm. Assuming that the diameter and the length are independently distributed, find the probability that a bearing has either diameter or length that differs from the mean by more than 0.02 cm.
The joint distribution of the diameters and lengths is given by:
Properties & Relations (7)
Marginal distributions are simply related to the component distributions:
One-dimensional marginal distributions:
Two-dimensional marginal distributions:
A product copula represents a product distribution:
The PDF is the product of the PDFs of the component distributions:
The CDF is the product of the CDFs of the component distributions:
The generating functions are products of generating functions of component distributions:
The components of the mean vector are the means of the component distributions:
A MultinormalDistribution is a product distribution when the covariance matrix is diagonal:
See Also
CopulaDistribution UniformDistribution Probability Covariance
Function Repository: ConditionalProductDistribution
Related Guides
Text
Wolfram Research (2010), ProductDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ProductDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "ProductDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ProductDistribution.html.
APA
Wolfram Language. (2010). ProductDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ProductDistribution.html
BibTeX
@misc{reference.wolfram_2025_productdistribution, author="Wolfram Research", title="{ProductDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ProductDistribution.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_productdistribution, organization={Wolfram Research}, title={ProductDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ProductDistribution.html}, note=[Accessed: 23-January-2026]}