TruncatedDistribution

TruncatedDistribution[{xmin,xmax},dist]

represents the distribution obtained by truncating the values of dist to lie between xmin and xmax.

TruncatedDistribution[{{xmin,xmax},{ymin,ymax},…},dist]

represents the distribution obtained by truncating the values of the multivariate distribution dist to lie between xmin and xmax, ymin and ymax, etc.

Details

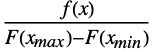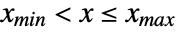  • The probability density for TruncatedDistribution[{xmin,xmax},dist] is given by for , where 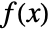is the PDF and 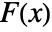is the CDF of dist, and is zero otherwise.
  • Common cases for {xmin,xmax} include:
  • {-∞,xmax}truncated from above
    {xmin,∞}truncated from below
    {xmin,xmax}doubly truncated
    {-∞,∞},Noneno truncation
  • TruncatedDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • TruncatedDistribution[{xmin,xmax},dist] represents a statistical distribution modeling data that is a constant multiple of the univariate distribution dist for all 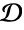in the interval 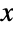and that is constantly 0 for 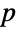. The terms non-truncated, truncated from below, truncated from above and doubly truncated are used to describe univariate truncations for which {xmin,xmax} has the form {-∞,∞}, {xmin,∞}, {-∞,xmax} and {xmin,xmax}, respectively, while univariate dist may be either continuous (e.g. NormalDistribution, GammaDistribution or BetaDistribution) or discrete (e.g. PoissonDistribution, BinomialDistribution or BernoulliDistribution) and may be defined in terms of transformations, censoring or truncations (by way of TransformedDistribution, CensoredDistribution and TruncatedDistribution, respectively) of known distributions.
  • The multivariate TruncatedDistribution[{{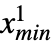,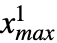},… ,{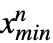,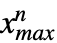}},dist] is defined analogously and thus represents the distribution of vectors 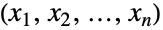taken from the multivariate distribution dist and whose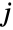 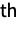^(th) component 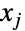is truncated to lie in the interval 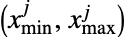. As in the univariate case, multivariate dist may again be either continuous (e.g. MultinormalDistribution) or discrete (e.g. MultivariateHypergeometricDistribution) and may also be defined as a copula or product (using CopulaDistribution and ProductDistribution, respectively) of known distributions.
  • Truncated distributions arise when datasets contain values that lie outside an interval considered "acceptable". For example, if the first 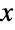people to file income taxes were to be audited from a pool of 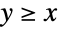taxpayers, then any statistical analysis performed on the audited returns would come in the form of truncated data, provided that no information was stored regarding the 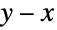taxpayers who avoided audits. Such data is common in fields such as survival analysis, finance, actuarial science and economics, and a variety of specialized statistical tools (e.g. truncated regression) exists to analyze such datasets.
  • TruncatedDistribution is often confused with CensoredDistribution, though the two are fundamentally different, in the sense that truncation distributes the probability over the truncation interval, while censoring puts the full probability at the end of the censoring interval. By definition, CensoredDistribution[{xmin,xmax},dist] is equivalent to TransformedDistribution[g,xdist], where g is given by Piecewise[{{0,x<=xmin},{h,xmin<x<xmax},{0,x>=xmax}}] for 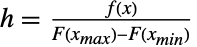, where 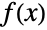is the PDF and 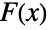is the CDF of dist.

Examples

open allclose all

Basic Examples  (3)

Simple truncated distributions:

Define a truncated univariate distribution:

Define a truncated multivariate distribution:

Scope  (35)

Basic Uses  (9)

Define various truncations for a univariate continuous distribution:

The resulting PDF is 0 outside the truncation region:

Define various truncations for a univariate discrete distribution:

The left endpoint is not included, but the right endpoint is included:

Define a right-truncated distribution:

Compare PDFs:

Define a left-truncated distribution:

Compare probability density functions:

Compare means:

Compare standard deviations:

Define a doubly truncated distribution:

Compare means:

Compare variances:

Define a truncated multivariate continuous distribution:

Compute the expectation of an expression for this distribution:

Find a few moments:

Define a truncated multivariate discrete distribution:

Compare probabilities for a point outside the truncation region:

Generate a random sample:

Compare the means:

Define a truncated multivariate discrete distribution:

Compare skewness:

Compare kurtosis:

Estimate a truncation interval using EstimatedDistribution:

Fit a truncated normal:

Parametric Distributions  (7)

Define a left-truncated continuous distribution:

Compare the probability density functions:

Cumulative distribution function of the truncated exponential distribution:

Statistical measures:

Compare to the original distribution:

Define a right-truncated discrete distribution:

Compare the PDFs:

The truncated distribution is the same as the following:

Define a truncation of a UniformDistribution:

Probability density function:

Compare to the uniform distribution defined on the truncation interval:

Define a truncation of a DiscreteUniformDistribution:

Probability density function:

Compare to the uniform distribution defined on the truncation interval:

Truncation does not include the left endpoint, hence the resulting discrete distribution:

Define a truncated binormal distribution:

Compare the PDFs for the binormal distribution and the truncated version:

Probability density function of the truncated binormal:

Characteristic function:

Define a discrete multivariate truncated distribution:

Perform statistical operations on this distribution:

Generate a set of pseudorandom numbers from a truncated distribution:

Compare the histogram to the PDF:

Nonparametric Distributions  (3)

Truncate a SmoothKernelDistribution:

Compare probability density functions:

Define a truncated EmpiricalDistribution:

Compare cumulative distribution functions:

Define a truncated HistogramDistribution:

Probability density function:

Derived Distributions  (10)

Define a truncated TruncatedDistribution:

Find a probability density function:

Identify as a truncated distribution:

Define a truncated CopulaDistribution:

Define a truncated MixtureDistribution:

Compare probability density functions:

Define a truncated OrderDistribution:

Find the probability that the maximum of a Poisson sample is greater than 6, assuming it is greater than 5:

Find the probability that the maximum is greater than 6 without assuming it is greater than 5:

Define a truncated TransformedDistribution:

Compare with the transformation of the truncated normal:

Define a truncated ParameterMixtureDistribution:

Compare PDFs:

Find the probabilities of most-likely values for both distributions:

Define a truncated ProductDistribution:

Compare the probability density functions:

Compare with the PDF of the product of the truncated distributions:

Define a truncated MarginalDistribution:

Compare the probability density functions:

Define a truncated CensoredDistribution:

Compare the probability density functions:

Truncation of a QuantityDistribution evaluates to QuantityDistribution:

Find mean temperature:

Automatic Simplifications  (6)

Continuous Distributions  (4)

GumbelDistribution truncated to a positive axis follows a GompertzMakehamDistribution:

NormalDistribution truncated to a positive axis follows a HalfNormalDistribution:

ParetoDistribution is closed under truncation:

UniformDistribution is closed under truncation:

Discrete Distributions  (2)

DiscreteUniformDistribution is closed under truncation:

ZipfDistribution is closed under truncation:

Applications  (5)

A grocery store orders pounds of produce for price per pound to be sold during the day. It sells the produce with margin per pound. The amount of produce sold in a day follows some distribution . The unsold produce is discarded at the end of the day. Compute so that it maximizes the daily profit:

Assuming 30% margin, and using LogNormalDistribution for distribution of demand:

The diameter of an American cranberry follows a normal distribution with mean 16 mm and standard deviation 1.6 mm. A fruit must be at least 15 mm across to be sold as whole; otherwise, it is used in the production of cranberry sauce. Find the size distribution of the fruits being sold as whole:

Compare probability density functions:

Find the average diameter of sold fruits:

The probability that a sold fruit is at least 18 mm in diameter:

Truncated distribution can be used to control display of long tail distributions. Consider a sample:

Fit a Pareto distribution to the data:

Compare the histogram of the sample with the PDF of the estimated distribution:

Due to the long tail, the histogram range has to be adjusted and the distribution truncated:

Consider the width of certain species of crab:

Fit a DagumDistribution to the data:

Compare the histogram to the PDF of the estimated distribution:

Usually the dimensions of the caught crab species fall in a certain range:

Fit left-truncated Dagum distribution to the data:

Compare log-likelihood values to see if the fit with a truncated distribution is better:

A company manufactures nails with length normally distributed and a mean of 0.5 inches. Given that the length of 50% of the produced nails differs less than 0.05 inches from the mean, find the standard deviation:

The standard deviation is found by requiring the probability of being within specs to equal 50%:

Plot to find the approximate value:

The standard deviation:

Properties & Relations  (7)

Truncating a distribution is equivalent to conditioning on an interval:

The PDF of a truncated distribution has nonzero values only inside the truncation interval:

Compare the density functions:

Construct the PDF of a truncated distribution by using properties of the underlying distribution:

Compare censoring with truncating for a discrete distribution:

While truncating, the weight from outside is evenly distributed over the truncation interval:

While censoring, the weight from outside is placed at the ends of the censoring interval:

Compare censoring and truncating of a continuous distribution:

While truncating, the probability is distributed over the truncation interval:

While censoring, the probability is put at the end of the censoring interval:

GompertzMakehamDistribution is related to a truncated WeibullDistribution:

Truncated GumbelDistribution is GompertzMakehamDistribution:

Neat Examples  (1)

Double truncation of a bivariate distribution:

Wolfram Research (2010), TruncatedDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TruncatedDistribution.html (updated 2016).

Text

Wolfram Research (2010), TruncatedDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TruncatedDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "TruncatedDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/TruncatedDistribution.html.

APA

Wolfram Language. (2010). TruncatedDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TruncatedDistribution.html

BibTeX

@misc{reference.wolfram_2024_truncateddistribution, author="Wolfram Research", title="{TruncatedDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/TruncatedDistribution.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_truncateddistribution, organization={Wolfram Research}, title={TruncatedDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/TruncatedDistribution.html}, note=[Accessed: 22-December-2024 ]}