ParetoDistribution

ParetoDistribution[k,α]

represents a Pareto distribution with minimum value parameter k and shape parameter α.

ParetoDistribution[k,α,μ]

represents a Pareto type II distribution with location parameter μ.

ParetoDistribution[k,α,γ,μ]

represents a Pareto type IV distribution with shape parameter γ.

Details

  • The probability density for value 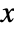in a Pareto distribution is proportional to 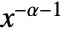for 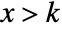, and is zero for . »
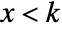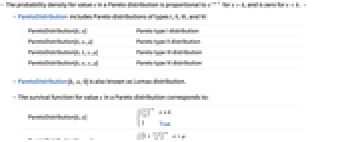
  • ParetoDistribution includes Pareto distributions of types I, II, III, and IV:
  • ParetoDistribution[k,α]Pareto type I distribution
    ParetoDistribution[k,α,μ]Pareto type II distribution
    ParetoDistribution[k,1,γ,μ]Pareto type III distribution
    ParetoDistribution[k,α,γ,μ]Pareto type IV distribution
  • ParetoDistribution[k,α,0] is also known as Lomax distribution.
  • The survival function for value 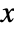in a Pareto distribution corresponds to:
  • ParetoDistribution[k,α](x/k)^(-alpha) x>=k; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
    ParetoDistribution[k,α,μ](1+(x-mu)/k)^(-alpha) x>mu; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
    ParetoDistribution[k,α,γ,μ](1+((x-mu)/k)^(1/gamma))^(-alpha) x>mu; 1 TemplateBox[{True, paclet:ref/True}, RefLink, BaseStyle -> {2ColumnTableMod}]
  • ParetoDistribution allows k, α, and γ to be any positive real numbers and μ any real number.
  • ParetoDistribution allows k and μ to be any quantities of the same unit dimensions, and α, γ to be dimensionless quantities. »
  • ParetoDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

  • ParetoDistribution represents a statistical distribution belonging to one of four types—type I, II, III, or IV—as determined by its argument structure. The overall shape of the probability density function (PDF) of a Pareto distribution varies significantly based on its arguments. For example, the PDF of types I and II Pareto distributions are monotonically decreasing while type IV distributions may have a single peak. In addition, the PDF of all types of ParetoDistribution are defined over a half-infinite interval and the tails of the PDF are "fat" in the sense that the PDF decreases as a power law rather than decreasing exponentially for large values 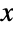. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
  • Pareto distributions originate with Italian economist Vilfredo Pareto, who noticed that approximately 80% of the peas in his garden were produced by roughly 20% of the pea pods. Later, Pareto observed that wealth distribution among nations followed a similar distribution, a result that led him to devise the so-called 80-20 rule (also called the Pareto principle), the basis for which is a type-I distribution corresponding to ParetoDistribution[k,α] with 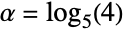. Pareto distributions also arise in a number of other mathematical and scientific contexts and are applicable to phenomena including hard disk error rates, price returns among stocks, and Bose–Einstein statistics.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Pareto distribution. Distributed[x,ParetoDistribution[k,α]], written more concisely as xParetoDistribution[k,α], can be used to assert that a random variable x is distributed according to a type-I Pareto distribution. Here, the positive parameter α is known as the Pareto index. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for type-I Pareto distributions may be given using PDF[ParetoDistribution[k,α]],x] and CDF[ParetoDistribution[k,α]],x], with similar expressions for type II, III, and IV distributions. In general, Pareto distributions have PDFs that are proportional to 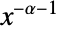. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a Pareto distribution, EstimatedDistribution to estimate a Pareto parametric distribution from given data, and FindDistributionParameters to fit data to a Pareto distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Pareto distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Pareto distribution.
  • TransformedDistribution can be used to represent a transformed Pareto distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Pareto distribution and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Pareto distributions.
  • ParetoDistribution is closely related to a number of other distributions. For example, the Pareto distribution is the continuous analogue of ZipfDistribution. As is result of its definition, the reciprocal of a Pareto‐distributed random variable follows the PowerDistribution. Furthermore, the distribution of the appropriately centered and scaled total values of independent samples of a Pareto-distributed random variable approaches a StableDistribution, while an exponential function of a random variable that follows ExponentialDistribution follows a ParetoDistribution. ParetoDistribution is also closely related to LogNormalDistribution, BenktanderWeibullDistribution, BeniniDistribution, BenktanderGibratDistribution, ChiSquareDistribution, PearsonDistribution, and BetaPrimeDistribution.

Examples

open allclose all

Basic Examples  (12)

Probability density function for Pareto I:

Cumulative distribution function for Pareto I:

Mean and variance of a Pareto I distribution:

Median of a Pareto I distribution:

Probability density function for Pareto II:

Cumulative distribution function for Pareto II:

Mean and variance of a Pareto II distribution:

Median of a Pareto II distribution:

Probability density function for Pareto IV:

Cumulative distribution function for a Pareto IV distribution:

Mean and variance of a Pareto IV distribution:

Median of a Pareto IV distribution:

Scope  (10)

Generate a sample of pseudorandom numbers from a Pareto distribution:

Compare its histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare the density histogram of the sample with the PDF of the estimated distribution:

Skewness of Pareto I and Pareto II distributions depends only on α where defined:

Limiting values:

Skewness of a Pareto IV distribution does not depend on the location parameter μ:

Kurtosis of Pareto I and Pareto II distributions is the same where defined:

Limiting values:

Kurtosis of a Pareto IV distribution does not depend on the location parameter μ:

Different moments of a Pareto I distribution with closed forms as functions of parameters:

Moment:

Closed form for symbolic order:

CentralMoment:

Closed form for symbolic order:

FactorialMoment:

Cumulant:

Different moments of a Pareto II distribution:

Moment:

Closed form for symbolic order:

CentralMoment:

FactorialMoment:

Cumulant:

Different moments of a Pareto IV distribution:

Moment:

CentralMoment:

FactorialMoment:

Cumulant:

Hazard function for Pareto I:

Hazard function for Pareto II:

Hazard function for Pareto IV:

Quantile function of a Pareto I distribution:

Quantile function of Pareto II:

Quantile function of Pareto IV:

Consistent use of Quantity in parameters yields QuantityDistribution:

Salary quartiles in this model:

Applications  (5)

ParetoDistribution as a long-tailed distribution can be used to model city population sizes:

Compare the histogram of population sizes with the PDF of the estimated distribution:

Find the probability that a city has a population of at least 10000:

Find the mean city size:

Simulate the population size of 20 randomly selected cities:

Use ParetoDistribution to model incomes at a large state university:

Adjust part-time salaries to full-time salaries and select nonzero values:

Fit Pareto distribution to the data:

Compare the histogram of the data to the PDF of the estimated distribution:

Find average income at the large state university:

Find the probability that a salary is at most $50000:

Find the probability that a salary is at least $150000:

Find the median salary:

Simulate the incomes for 100 randomly selected employees of such a university:

The lifetime of a device follows ParetoDistribution:

Find the reliability of the device:

Find the average lifetime of this device:

Find the probability that the device will be operational for more than 6 years:

Find the failure rate of the device:

Consider earthquake magnitudes recorded in the US from 1935 to 1989:

The integer parts of the magnitudes recorded on a Richter scale can be modeled with a ParetoDistribution:

Compare the histogram of the magnitudes with the fitted distribution:

Find the probability of an earthquake with magnitude at least 6 on the Richter scale:

Find the average magnitude:

Simulate the next 30 earthquakes:

Use truncated Pareto IV distribution to define Bradford distribution:

Find the limit of density function when the shape parameter tends to 0:

Substitute to simplify constants:

Define Bradford distribution:

Bradford probability density function:

Cumulative distribution function:

Generate random numbers:

Properties & Relations  (20)

Pareto distribution is closed under translation:

The probability density and random variable have a power-law relationship:

The family of Pareto distribution is closed under the minimum:

For different values of shape parameter:

Special case of truncation:

Relationships to other distributions:

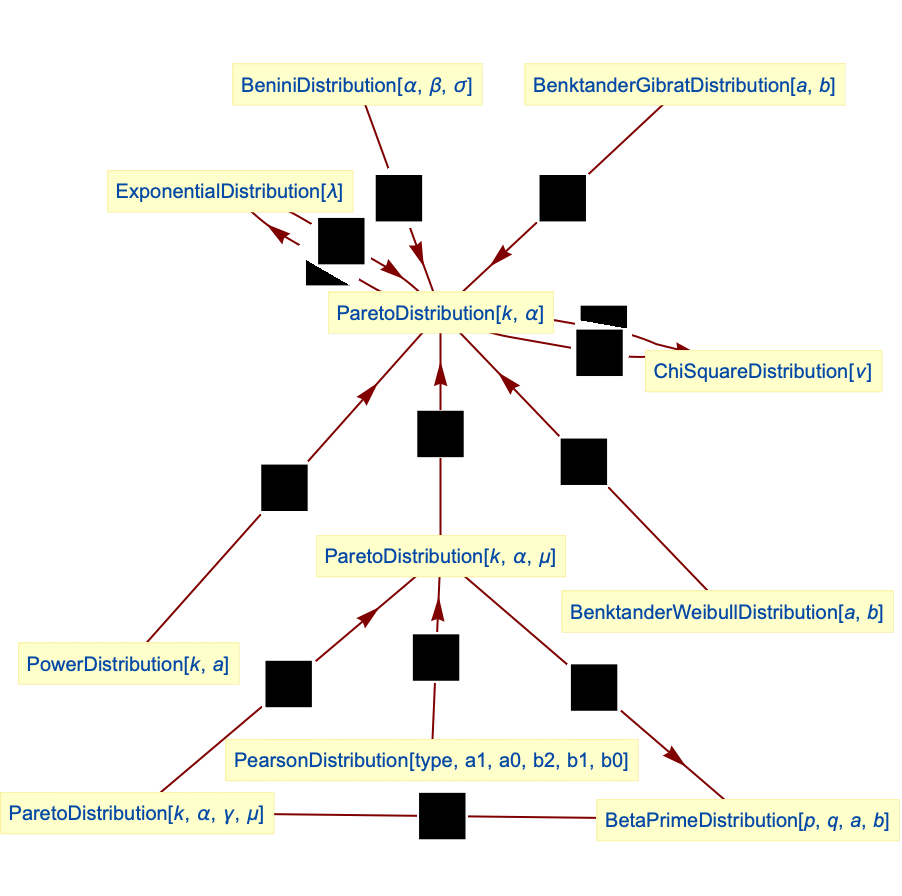
Pareto type II distribution is a special case of type 6 PearsonDistribution:

Pareto type I distribution is a special case of BeniniDistribution:

Pareto II distribution simplifies to Pareto I for :

Pareto IV distribution simplifies to Pareto II for :

Pareto distribution is a distribution of an inverse of PowerDistribution:

A Pareto distribution is the limiting case of the BenktanderGibratDistribution:

A Pareto distribution is the limiting case of the BenktanderWeibullDistribution:

ChiSquareDistribution is a transformation of Pareto-distributed variates:

ChiSquareDistribution is a transformation of Pareto-distributed variates:

Pareto distribution is a transformation of ExponentialDistribution:

Transformation of a Pareto distribution yields ExponentialDistribution:

Pareto II is related to BetaPrimeDistribution:

Pareto IV is related to BetaPrimeDistribution:

ParetoDistribution can be obtained as a quotient of ExponentialDistribution and ErlangDistribution:

ParetoDistribution can be obtained as a quotient of ExponentialDistribution and GammaDistribution:

Possible Issues  (3)

ParetoDistribution is not defined when k is not a real number:

ParetoDistribution is not defined when α is not a positive real number:

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Pareto II distribution for is not Pareto I:

Pareto II distribution simplifies to Pareto I for :

Neat Examples  (1)

PDFs for different γ values with CDF contours:

Wolfram Research (2007), ParetoDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ParetoDistribution.html (updated 2016).

Text

Wolfram Research (2007), ParetoDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ParetoDistribution.html (updated 2016).

CMS

Wolfram Language. 2007. "ParetoDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ParetoDistribution.html.

APA

Wolfram Language. (2007). ParetoDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParetoDistribution.html

BibTeX

@misc{reference.wolfram_2024_paretodistribution, author="Wolfram Research", title="{ParetoDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ParetoDistribution.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_paretodistribution, organization={Wolfram Research}, title={ParetoDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ParetoDistribution.html}, note=[Accessed: 22-December-2024 ]}