Median

Median[data]

gives the median estimate of the elements in data.

Median[dist]

gives the median of the distribution dist.

Details

  • Median is a robust location estimator, which means it not very sensitive to outliers.
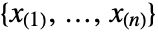  • For a vector data , the median can be thought of as the "middle value".
  • Formally, when data is sorted as 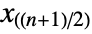, the median is given by center element 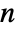if 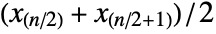is odd and the mean of the two center elements 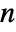if 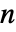is even.
  • Median[data] is equivalent to Quantile[data,1/2,{{1/2,0},{0,1}}].
  • For matrix data, the median is computed for each column vector with Median[{{x1,y1,…},{x2,y2,…},…}] equivalent to {Median[{x1,x2,…}],Median[{y1,y2,…}],…}. »
  • For array data, median is equivalent to ArrayReduce[Median,data,1]. »
  • ↓↓↓↓↓
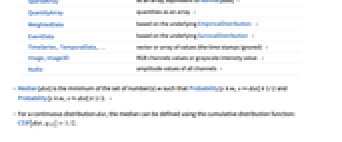
  • The data can have the following additional forms and interpretations:
  • Associationthe values (the keys are ignored) »
    SparseArrayas an array, equivalent to Normal[data] »
    QuantityArrayquantities as an array »
    WeightedDatabased on the underlying EmpiricalDistribution »
    EventDatabased on the underlying SurvivalDistribution »
    TimeSeries, TemporalData, …vector or array of values (the time stamps ignored) »
    Image,Image3DRGB channels values or grayscale intensity value »
    Audioamplitude values of all channels »
  • Median[dist] is the minimum of the set of number(s) m such that Probability[x≤m,xdist]≥1/2 and Probability[x≥m,xdist]≥1/2. »
  • For a continuous distribution dist, the median can be defined using the cumulative distribution function: CDF[dist,q_(1/2)]=1/2.
  • Median[dist] is equivalent to Quantile[dist,1/2].
  • For a random process proc, the median function 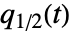can be computed for slice distribution at time t, SliceDistribution[proc,t], as Median[SliceDistribution[proc,t]]. »

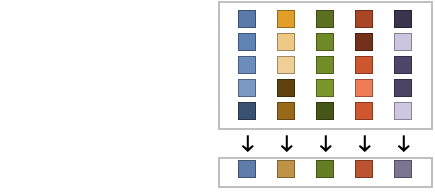
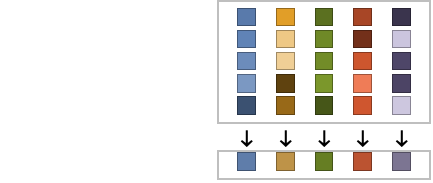
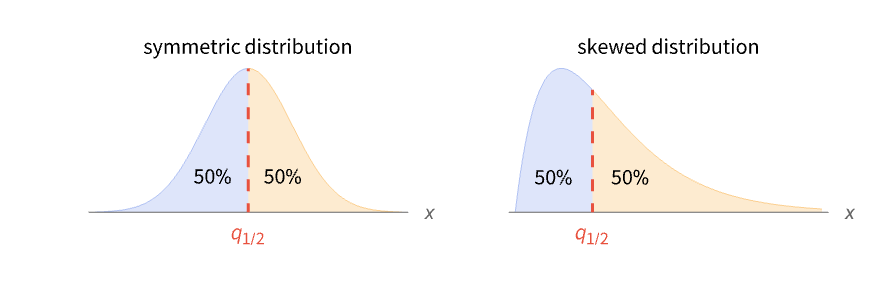
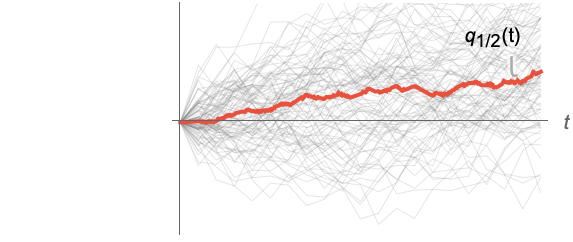
Examples

open allclose all

Basic Examples  (3)

Find the middle value in the list:

Average the two middle values:

Median of a parametric distribution:

Scope  (19)

Basic Uses  (8)

Exact input yields exact output:

Approximate input yields approximate output:

Find the median of WeightedData:

Find the median of EventData:

Find the median of TemporalData:

Find the median of a TimeSeries:

The median depends only on the values:

Find a three-element moving median:

Find the median of data involving quantities:

Array Data  (5)

Median for a matrix gives columnwise medians:

Median for a tensor gives columnwise medians at the first level:

Works with large arrays:

When the input is an Association, Median works on its values:

SparseArray data can be used just like dense arrays:

Find median of a QuantityArray:

Image and Audio Data  (2)

Channel-wise median value of an RGB image:

Median intensity value of a grayscale image:

Median amplitude of all amplitude values of all channels:

Distributions and Processes  (4)

Find the median for a parametric distribution:

Median for a derived distribution:

Data distribution:

Median for distributions with quantities:

Median function for a time slice of a random process:

Applications  (7)

The median represents the center of a distribution:

The median for a distribution without a single mode:

Find the median length, in miles, for 141 major rivers in North America:

Plot a Histogram for the data:

Probability that the length exceeds 90% of the median:

Smooth an irregularly spaced time series using a moving median:

A 90-day moving median:

Obtain a robust estimate of location when outliers are present:

Extreme values have a large influence on the Mean:

Compute medians for slices of a collection of paths of a random process:

Choose a few slice times:

Plot medians over these paths:

Find the median height for the children in a class:

Properties & Relations  (7)

Median is equivalent to a parametrized Quantile:

For nearly symmetric samples, Median and Mean are nearly the same:

For univariate data, Median coincides with SpatialMedian:

The Median of absolute deviations from the Median is MedianDeviation:

MovingMedian is a sequence of medians:

For any distribution, there is InverseCDF[dist,1/2]=Median[dist]:

Similarly for InverseSurvivalFunction:

For a continuous distribution, there is CDF[dist,Median[dist]]=1/2:

Similarly for SurvivalFunction:

For discrete distributions, the identity does not hold:

Possible Issues  (2)

Median requires numeric values:

Median of data computed via Quantile does not always agree with Median:

Calculate median directly:

Specify linear interpolation parameters in Quantile:

Neat Examples  (1)

The distribution of Median estimates for 20, 100, and 300 samples:

Wolfram Research (2003), Median, Wolfram Language function, https://reference.wolfram.com/language/ref/Median.html (updated 2023).

Text

Wolfram Research (2003), Median, Wolfram Language function, https://reference.wolfram.com/language/ref/Median.html (updated 2023).

CMS

Wolfram Language. 2003. "Median." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/Median.html.

APA

Wolfram Language. (2003). Median. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Median.html

BibTeX

@misc{reference.wolfram_2023_median, author="Wolfram Research", title="{Median}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Median.html}", note=[Accessed: 30-September-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_median, organization={Wolfram Research}, title={Median}, year={2023}, url={https://reference.wolfram.com/language/ref/Median.html}, note=[Accessed: 30-September-2023 ]}