InverseCDF

InverseCDF[dist,q]

gives the inverse of the cumulative distribution function for the distribution dist as a function of the variable q.

Details

  • The inverse CDF at q is also referred to as the q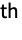^(th) quantile of a distribution.
  • For a continuous distribution dist the inverse CDF at q is the value x such that CDF[dist,x]q.
  • For a discrete distribution dist the inverse CDF at q is the smallest integer x such that CDF[dist,x]≥q.
  • The value q can be symbolic or any number between 0 and 1.

Examples

open allclose all

Basic Examples  (2)

The inverse CDF for a continuous univariate distribution:

The inverse CDF for a discrete univariate distribution:

Scope  (12)

Parametric Distributions  (5)

Obtain exact numeric results:

Obtain a machine-precision result:

Obtain a result at any precision for a continuous distribution:

Obtain a symbolic expression for the InverseCDF:

Plot the InverseCDF:

Derived Distributions  (3)

InverseCDF for a truncated distribution:

Quadratic transformation of an exponential distribution:

Censored distribution:

Nonparametric Distributions  (2)

InverseCDF for nonparametric distributions:

Compare with the value for the underlying parametric distribution:

Plot the InverseCDF for a histogram distribution:

Random Processes  (2)

InverseCDF for the SliceDistribution of a random process:

Find the InverseCDF of TemporalData at some time t=0.5:

Find the InverseCDF for a range of times together with all the simulations:

Generalizations & Extensions  (2)

InverseCDF threads element-wise over lists:

Specify the argument using units of percent or permil:

Applications  (4)

Generate a random number from a distribution:

Find the quartiles of a distribution:

Generate random data for a distribution:

Compute mean of a distribution by integrating inverse CDF function:

Compute mean of 5:3 order statistics of the distribution:

Properties & Relations  (7)

InverseCDF is equivalent to Quantile for univariate distributions:

InverseCDF[,p] is continuous and strictly increasing for 0≤p≤1 and continuous:

InverseCDF[,p] is piecewise constant and increasing for 0≤p≤1 and discrete:

The function is continuous from the left, and discontinuous from the right:

InverseCDF[,p] is left-continuous and increasing for 0≤p≤1 and mixed:

InverseCDF[,CDF[,x]]x for a continuous distribution :

CDF[,InverseCDF[,p]]p for a continuous distribution :

InverseCDF[,CDF[,x]]≤x for a discrete distribution :

CDF[,InverseCDF[,p]]≥p for a discrete distribution :

TransformedDistribution[InverseCDF[,p],pUniformDistribution[]] is :

This can be used to generate random variates:

Possible Issues  (2)

Symbolic closed forms do not exist for some distributions:

Numerical evaluation works:

Substitution of invalid values into symbolic outputs gives results that are not meaningful:

When giving the input as argument complete checking is done:

Wolfram Research (2007), InverseCDF, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseCDF.html.

Text

Wolfram Research (2007), InverseCDF, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseCDF.html.

CMS

Wolfram Language. 2007. "InverseCDF." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseCDF.html.

APA

Wolfram Language. (2007). InverseCDF. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseCDF.html

BibTeX

@misc{reference.wolfram_2024_inversecdf, author="Wolfram Research", title="{InverseCDF}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/InverseCDF.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversecdf, organization={Wolfram Research}, title={InverseCDF}, year={2007}, url={https://reference.wolfram.com/language/ref/InverseCDF.html}, note=[Accessed: 21-December-2024 ]}