Mean

Mean[data]

gives the mean estimate of the elements in data.

Mean[dist]

gives the mean of the distribution dist.

Details

  • Mean is also known as an expectation or average.
  • Mean is a location measure for data or distributions.
  • For VectorQ data 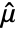, the mean estimate 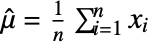is given by .
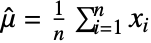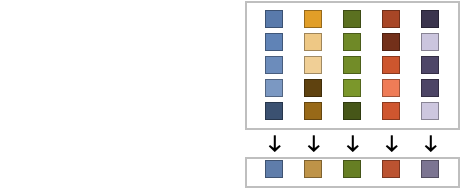
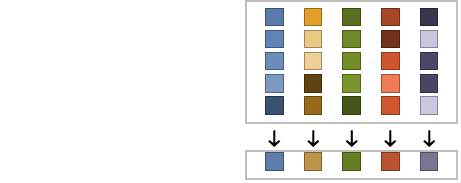
  • For MatrixQ data, the mean estimate 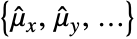is computed for each column vector with Mean[{{x1,y1,…},{x2,y2,…},…}] equivalent to {Mean[{x1,x2,…}],Mean[{y1,y2,…}],…}. »
  • For ArrayQ data, the mean estimate is equivalent to ArrayReduce[Mean,data,1]. »
  • For WeightedData[{x1,x2,…},{w1,w2,…}], the mean estimate is given by . »
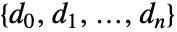  • Mean handles both numerical and symbolic data.
  • The data can have the following additional forms and interpretations:
  • Associationthe values (the keys are ignored) »
    WeightedDataweighted mean, based on the underlying EmpiricalDistribution »
    EventDatabased on the underlying SurvivalDistribution »
    TimeSeries, TemporalData, …vector or array of values (the time stamps ignored) »
    Image,Image3DRGB channels values or grayscale intensity value »
    Audioamplitude values of all channels »
    DateObject,TimeObjectlist of dates or list of times »
  • For a list of dates 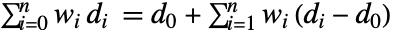, the mean is given by 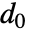, which is date 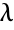plus sum of durations .
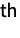  • For a univariate distribution dist, the mean is given by μ=Expectation[x,xdist]. »
  • For multivariate distribution dist, the mean is given by {μx ,μy,…}=Expectation[{x,y,…},{x,y,…}dist]. »
  • For a random process proc, the mean function can be computed for slice distribution at time t, SliceDistribution[proc,t], as μ[t]=Mean[SliceDistribution[proc,t]]. »

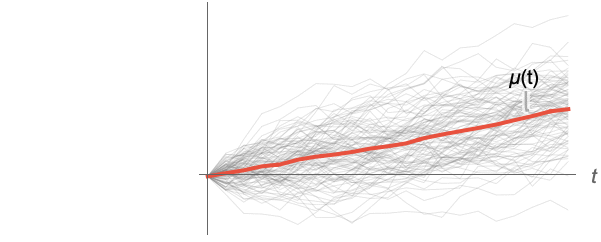
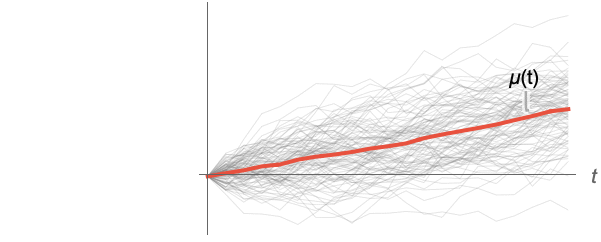
Examples

open allclose all

Basic Examples  (5)

Mean of numeric values:

Mean of symbolic values:

Means of elements in each column:

Mean of a list of dates:

Mean of a parametric distribution:

Scope  (22)

Basic Uses  (6)

Exact input yields exact output:

Approximate input yields approximate output:

Find the mean of WeightedData:

Find the mean of EventData:

Find the mean of a TimeSeries:

The mean depends only on the values:

Compute a weighted mean:

Find the mean of data involving quantities:

Array Data  (5)

Mean for a matrix gives columnwise means:

Mean for a arrays gives columnwise means at the first level:

Works with large arrays:

When the input is an Association, Mean works on its values:

SparseArray data can be used just like dense arrays:

Find mean of a QuantityArray:

Image and Audio Data  (2)

Channel-wise mean value of an RGB image:

Mean intensity value of a grayscale image:

On audio objects, Mean works channel-wise:

Date and Time  (4)

Compute mean of dates:

Compute the weighted mean of dates:

Compute the mean of dates given in different calendars:

The mean is given in one of the input calendars:

Compute the mean of times:

List of times with different time zone specifications:

Distributions and Processes  (5)

Find the mean for univariate distributions:

Multivariate distributions:

Mean for derived distributions:

Data distribution:

Mean for distributions with quantities:

Mean function for a continuous-time random and discrete-state process:

Find the mean of TemporalData at some time t=0.5:

Find the mean function together with all the simulations:

Applications  (11)

Basic Applications  (5)

The mean represents the center of mass for a distribution:

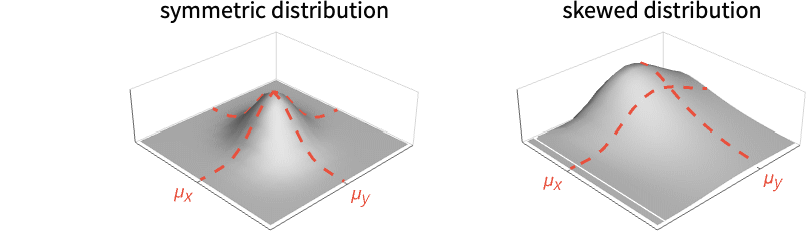
The mean for distributions without a single mode:

The mean for multivariate distributions:

Mean values of cells in a sequence of steps of 2D cellular automaton evolution:

Compute means for slices of a collection of paths of a random process:

Choose a few slice times:

Plot means over these paths:

Applications  (6)

Find the mean height for the children in a class:

Find the mean height for the children in a class:

Find the mean strength for 480 samples of ceramic material:

Plot a Histogram for the data with mean position highlighted:

Compute the probability that the strength exceeds the mean:

Compute the mean lifetime for a quantity subject to exponential decay with rate :

Smooth an irregularly spaced time series by computing a moving mean:

A 90-day moving mean:

A vacuum system in a small electron accelerator contains 20 vacuum bulbs arranged in a circle. The vacuum system fails if at least 3 adjacent vacuum bulbs fail:

Plot the survival function:

Compute the mean time to failure:

Properties & Relations  (17)

Mean is Total divided by Length:

Mean is equivalent to a 1‐norm divided by Length for positive values:

Mean of WeightedData is equivalent to the mean of the EmpiricalDistribution of the data:

Mean of EventData is equivalent to the mean of the SurvivalDistribution of the data:

For nearly symmetric samples, Mean and Median are nearly the same:

The Mean of absolute deviations from the Mean is MeanDeviation:

Mean is logarithmically related to GeometricMean for positive values:

Mean is the inverse of HarmonicMean of the inverse of the data:

The square root of Mean of the data squared is RootMeanSquare:

The n^(th) CentralMoment is the Mean of deviations raised to the n^(th) power:

Variance is a scaled Mean of squared deviations from the Mean:

Expectation for a list is a Mean:

MovingAverage is a sequence of means:

A 0% TrimmedMean is the same as Mean:

The Expectation of a random variable in a distribution is the Mean:

LocationTest tests whether the mean is close to 0:

The probability () value:

LocationEquivalenceTest tests for equivalence of means in two or more datasets:

The probability () value:

Possible Issues  (1)

Outliers can have a disproportionate effect on Mean:

Use TrimmedMean to ignore a fraction of the smallest and largest elements:

Use Median as something much less sensitive to outliers:

Neat Examples  (1)

The distribution of Mean estimates for 10, 100, and 300 samples:

Wolfram Research (2003), Mean, Wolfram Language function, https://reference.wolfram.com/language/ref/Mean.html (updated 2024).

Text

Wolfram Research (2003), Mean, Wolfram Language function, https://reference.wolfram.com/language/ref/Mean.html (updated 2024).

CMS

Wolfram Language. 2003. "Mean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Mean.html.

APA

Wolfram Language. (2003). Mean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Mean.html

BibTeX

@misc{reference.wolfram_2025_mean, author="Wolfram Research", title="{Mean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Mean.html}", note=[Accessed: 05-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_mean, organization={Wolfram Research}, title={Mean}, year={2024}, url={https://reference.wolfram.com/language/ref/Mean.html}, note=[Accessed: 05-May-2025 ]}