StandardDeviation

StandardDeviation[data]

gives the standard deviation estimate of the elements in data.

StandardDeviation[dist]

gives the standard deviation of the distribution dist.

Details

  • StandardDeviation is also known as volatility.
  • StandardDeviation measures dispersion from the mean of data or distributions.
  • For vector data with 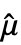=Mean[data], the standard deviation estimate 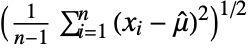is given by 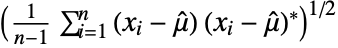for reals and 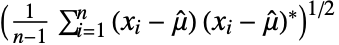for complexes.
  • For matrix data, the standard deviation estimate 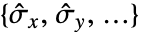is computed for each column vector with StandardDeviation[{{x1,y1,…},{x2,y2,…},…}] equivalent to {StandardDeviation[{x1,x2,…}],StandardDeviation[{y1,y2,…}]}. »
  • For array data, standard deviation is equivalent to ArrayReduce[StandardDeviation,data,1]. »
  • ↓↓↓↓↓
  • For a real weighted WeightedData[{x1,x2,…},{w1,w2,…}], the standard deviation is given by . »
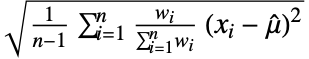  • StandardDeviation handles both numerical and symbolic data.
  • The data can have the following additional forms and interpretations:
  • Associationthe values (the keys are ignored) »
    SparseArrayas an array, equivalent to Normal[data] »
    QuantityArrayquantities as an array »
    WeightedDataweighted variance, based on the underlying EmpiricalDistribution »
    EventDatabased on the underlying SurvivalDistribution »
    TimeSeries, TemporalData, …vector or array of values (the time stamps ignored) »
    Image,Image3DRGB channel's values or grayscale intensity value »
    Audioamplitude values of all channels »
  • For a univariate distribution dist, the standard deviation is given by σ=Expectation[(x-μ)2,xdist]1/2 with μ=Mean[dist]. »
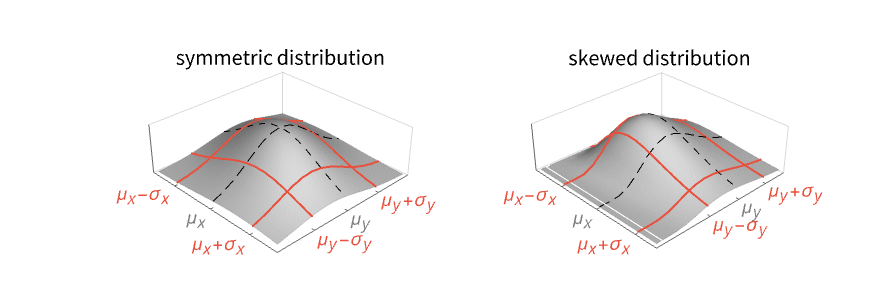
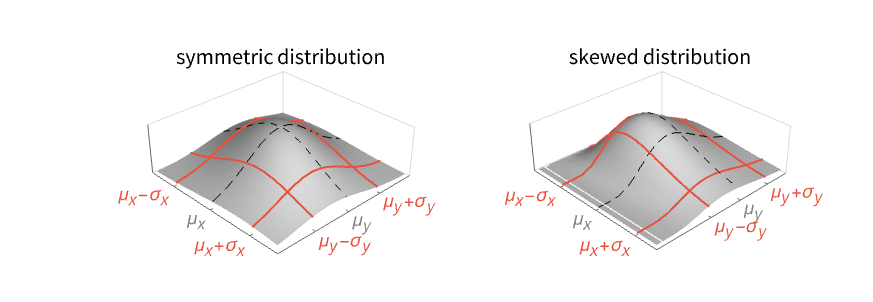
  • For multivariate distribution dist, the standard deviation is given by {σx,σy,…}=Expectation[{(x-μx)2,(y-μy)2,…},{x,y,…}dist]1/2. »
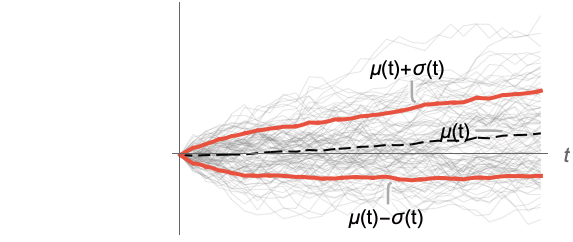
  • For a random process proc, the standard deviation function 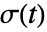can be computed for slice distribution at time t, SliceDistribution[proc,t], as σ[t]=StandardDeviation[SliceDistribution[proc,t]]. »

Examples

open allclose all

Basic Examples  (3)

Standard deviation of a list of numbers:

Standard deviation of elements in each column:

Standard deviation of a parametric distribution:

Scope  (19)

Basic Uses  (8)

Exact input yields exact output:

Approximate input yields approximate output:

Find the standard deviation of WeightedData:

Find the standard deviation of EventData:

Find the standard deviation of TemporalData:

Find the standard deviation of a TimeSeries:

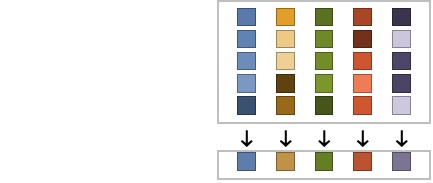
The standard deviation depends only on the values:

Find a three-element moving standard deviation:

Find the standard deviation of data involving quantities:

Array Data  (5)

StandardDeviation for a matrix gives columnwise standard deviations:

StandardDeviation for a tensor gives columnwise standard deviations at the first level:

Works with large arrays:

When the input is an Association, StandardDeviation works on its values:

SparseArray data can be used just like dense arrays:

Find the standard deviation of a QuantityArray:

Image and Audio Data  (2)

Channelwise standard deviation of an RGB image:

Standard deviation of a grayscale image:

On audio objects, StandardDeviation works channelwise:

Distributions and Processes  (4)

Find the standard deviation for univariate distributions:

Multivariate distributions:

Standard deviation for derived distributions:

Data distribution:

Standard deviation for distributions with quantities:

Standard deviation function for a random process:

Applications  (7)

StandardDeviation is a measure of dispersion:

Transform data to have mean 0 and unit variance:

Identify periods of high volatility in the S&P 500 using a five-year moving standard deviation:

Find the mean and standard deviation for the number of cycles to failure of deep-groove ball-bearings:

Plot the data:

Probability that the values lie within two standard deviations of the mean:

Investigate weak stationarity of the process data by analyzing standard deviations of slices:

Use a larger plot range to see how relatively small the variations are:

Compute standard deviation for slices of a collection of paths of a random process:

Choose a few slice times:

Compute standard deviations and means:

Create a standard deviation band around the mean:

Plot standard deviations around the mean over these paths:

Find the standard deviation of the heights for the children in a class:

The heights within one standard deviation from the mean:

Properties & Relations  (9)

The square of StandardDeviation is Variance:

StandardDeviation is a scaled Norm of deviations from the Mean:

StandardDeviation is the square root of a scaled CentralMoment:

StandardDeviation is a scaled RootMeanSquare of the deviations:

StandardDeviation is the square root of a scaled Mean of squared deviations:

StandardDeviation as a scaled EuclideanDistance from the Mean:

StandardDeviation squared is less than MeanDeviation if all absolute deviations are less than 1:

StandardDeviation squared is greater than MeanDeviation if all absolute deviations are greater than 1:

StandardDeviation of a random variable as the square root of Variance:

Neat Examples  (1)

The distribution of StandardDeviation estimates for 20, 100, and 300 samples:

Wolfram Research (2003), StandardDeviation, Wolfram Language function, https://reference.wolfram.com/language/ref/StandardDeviation.html (updated 2023).

Text

Wolfram Research (2003), StandardDeviation, Wolfram Language function, https://reference.wolfram.com/language/ref/StandardDeviation.html (updated 2023).

CMS

Wolfram Language. 2003. "StandardDeviation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/StandardDeviation.html.

APA

Wolfram Language. (2003). StandardDeviation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StandardDeviation.html

BibTeX

@misc{reference.wolfram_2023_standarddeviation, author="Wolfram Research", title="{StandardDeviation}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/StandardDeviation.html}", note=[Accessed: 01-December-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_standarddeviation, organization={Wolfram Research}, title={StandardDeviation}, year={2023}, url={https://reference.wolfram.com/language/ref/StandardDeviation.html}, note=[Accessed: 01-December-2023 ]}