RootMeanSquare

RootMeanSquare[list]

gives the root mean square of values in list.

RootMeanSquare[dist]

gives the root mean square of the distribution dist.

Details

  • RootMeanSquare measures scale of data or distributions.
  • RootMeanSquare[list] gives the square root of the second sample moment.
  • For the list {x1,x2,…,xn}, the root mean square is given by .
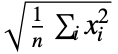  • RootMeanSquare handles both numerical and symbolic data.
  • RootMeanSquare[{{x1,y1,…},{x2,y2,…},…}] gives {RootMeanSquare[{x1,x2,…}],RootMeanSquare[{y1,y2,…}]}.
  • RootMeanSquare[dist] is equivalent to Sqrt[Expectation[x2,xdist]].

Examples

open allclose all

Basic Examples  (3)

RootMeanSquare of a list:

RootMeanSquare of columns of a matrix:

RootMeanSquare of a parametric distribution:

Scope  (14)

Data  (10)

Exact input yields exact output:

Approximate input yields approximate output:

RootMeanSquare for a matrix gives columnwise means:

Works with large arrays:

SparseArray data can be used just like dense arrays:

Compute results for a SparseArray:

RootMeanSquare for WeightedData:

RootMeanSquare for EventData:

RootMeanSquare for TimeSeries:

The root mean square depends only on the values:

RootMeanSquare for data involving quantities:

Distributions and Processes  (4)

Find the RootMeanSquare for univariate distributions:

Multivariate distributions:

RootMeanSquare for derived distributions:

Data distribution:

RootMeanSquare for distributions with quantities:

RootMeanSquare for a random process:

Applications  (3)

Root mean square error for a linear fit:

Sample a periodic signal:

Compute the root mean square value of the sample:

Compare with the exact value:

Find the root mean square value for the heights of children in a class:

Properties & Relations  (7)

RootMeanSquare is the square root of the Mean of the data squared:

RootMeanSquare is equivalent to a scaled Norm:

RootMeanSquare of deviations is equivalent to a scaled StandardDeviation:

RootMeanSquare of deviations is the square root of a CentralMoment:

RootMeanSquare is a scaled EuclideanDistance from the Mean:

RootMeanSquare of a random variable is the square root of an Expectation:

RootMeanSquare is a measure of scale:

Wolfram Research (2007), RootMeanSquare, Wolfram Language function, https://reference.wolfram.com/language/ref/RootMeanSquare.html (updated 2017).

Text

Wolfram Research (2007), RootMeanSquare, Wolfram Language function, https://reference.wolfram.com/language/ref/RootMeanSquare.html (updated 2017).

CMS

Wolfram Language. 2007. "RootMeanSquare." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.

APA

Wolfram Language. (2007). RootMeanSquare. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootMeanSquare.html

BibTeX

@misc{reference.wolfram_2024_rootmeansquare, author="Wolfram Research", title="{RootMeanSquare}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RootMeanSquare.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rootmeansquare, organization={Wolfram Research}, title={RootMeanSquare}, year={2017}, url={https://reference.wolfram.com/language/ref/RootMeanSquare.html}, note=[Accessed: 18-December-2024 ]}