RootMeanSquare
✖
RootMeanSquare
更多信息
- RootMeanSquare 测量数据规模或分布.
- RootMeanSquare[list] 给出第二样本矩的平方根.
- 对于 {x1,x2,…,xn},均方根由
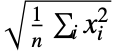 给出.
给出. - RootMeanSquare 处理数值和符号数据.
- RootMeanSquare[{{x1,y1,…},{x2,y2,…},…}] 给出 {RootMeanSquare[{x1,x2,…}],RootMeanSquare[{y1,y2,…}]}.
- RootMeanSquare[dist] 等价于 Sqrt[Expectation[x2,xdist]].
范例
打开所有单元关闭所有单元基本范例 (3)常见实例总结
一个列表的 RootMeanSquare :
https://wolfram.com/xid/0g7itfcdyf2-xif
矩阵列的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-vu6sr
参数分布的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-f8uw3n
范围 (14)标准用法实例范围调查
数据 (10)
https://wolfram.com/xid/0g7itfcdyf2-ug7y2
https://wolfram.com/xid/0g7itfcdyf2-bcry2t
https://wolfram.com/xid/0g7itfcdyf2-ksx55
https://wolfram.com/xid/0g7itfcdyf2-d02ofx
矩阵的 RootMeanSquare 逐列给出均值:
https://wolfram.com/xid/0g7itfcdyf2-81exum
https://wolfram.com/xid/0g7itfcdyf2-hoea5t
https://wolfram.com/xid/0g7itfcdyf2-njdm69
可以像使用稠密数组一样使用 SparseArray 数据:
https://wolfram.com/xid/0g7itfcdyf2-n691tv
https://wolfram.com/xid/0g7itfcdyf2-drrysl
对于 SparseArray 的计算结果:
https://wolfram.com/xid/0g7itfcdyf2-d3sclc
https://wolfram.com/xid/0g7itfcdyf2-ma7jv
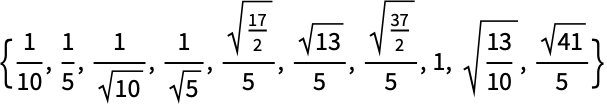
WeightedData 的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-d0wc9z
https://wolfram.com/xid/0g7itfcdyf2-f1vfw
https://wolfram.com/xid/0g7itfcdyf2-qyv0h
https://wolfram.com/xid/0g7itfcdyf2-e67u14
https://wolfram.com/xid/0g7itfcdyf2-or2nrz

https://wolfram.com/xid/0g7itfcdyf2-hf056t

https://wolfram.com/xid/0g7itfcdyf2-ikztk4
涉及量的数据的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-jopin9
https://wolfram.com/xid/0g7itfcdyf2-e8c21s
分布和过程 (4)
求单变量分布的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-rxz55
https://wolfram.com/xid/0g7itfcdyf2-hbq28j
https://wolfram.com/xid/0g7itfcdyf2-ek075b
https://wolfram.com/xid/0g7itfcdyf2-lzwoz3
导出分布的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-rgc72x
https://wolfram.com/xid/0g7itfcdyf2-byqvvz
https://wolfram.com/xid/0g7itfcdyf2-215ry
https://wolfram.com/xid/0g7itfcdyf2-fq5ptk
含有量的分布的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-dqsioj
https://wolfram.com/xid/0g7itfcdyf2-b53jwg
随机过程的 RootMeanSquare:
https://wolfram.com/xid/0g7itfcdyf2-fugn
https://wolfram.com/xid/0g7itfcdyf2-g9pmgp
应用 (3)用该函数可以解决的问题范例
https://wolfram.com/xid/0g7itfcdyf2-lqzjie
https://wolfram.com/xid/0g7itfcdyf2-p1u03
https://wolfram.com/xid/0g7itfcdyf2-cab9e7
https://wolfram.com/xid/0g7itfcdyf2-cwptf9
https://wolfram.com/xid/0g7itfcdyf2-dkujrt
https://wolfram.com/xid/0g7itfcdyf2-yv2c2
https://wolfram.com/xid/0g7itfcdyf2-csnxk
https://wolfram.com/xid/0g7itfcdyf2-ekvqot
https://wolfram.com/xid/0g7itfcdyf2-c3rp5t
https://wolfram.com/xid/0g7itfcdyf2-cevfij
https://wolfram.com/xid/0g7itfcdyf2-fllmtw
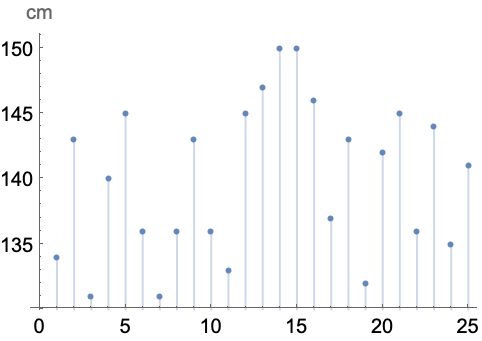
https://wolfram.com/xid/0g7itfcdyf2-celepo
https://wolfram.com/xid/0g7itfcdyf2-cny2bx
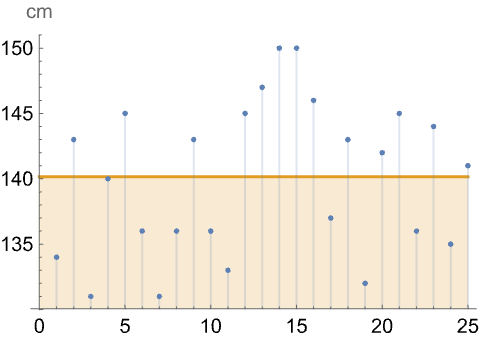
属性和关系 (7)函数的属性及与其他函数的关联
RootMeanSquare 是数据平方的 Mean 的平方根:
https://wolfram.com/xid/0g7itfcdyf2-793v1
https://wolfram.com/xid/0g7itfcdyf2-b9x4up
https://wolfram.com/xid/0g7itfcdyf2-bhsxlb
RootMeanSquare 等价于经过缩放的 Norm:
https://wolfram.com/xid/0g7itfcdyf2-jxw4y8
https://wolfram.com/xid/0g7itfcdyf2-drqfrx
https://wolfram.com/xid/0g7itfcdyf2-cuwc0b
偏差的 RootMeanSquare 等价于经过缩放的 StandardDeviation:
https://wolfram.com/xid/0g7itfcdyf2-m0xfm
https://wolfram.com/xid/0g7itfcdyf2-hh6mz4
https://wolfram.com/xid/0g7itfcdyf2-i5cfjy
偏差的 RootMeanSquare 是 CentralMoment 的平方根:
https://wolfram.com/xid/0g7itfcdyf2-dso2q7
https://wolfram.com/xid/0g7itfcdyf2-vy95m
https://wolfram.com/xid/0g7itfcdyf2-hfsstq
RootMeanSquare 是距 Mean 的经过缩放的 EuclideanDistance:
https://wolfram.com/xid/0g7itfcdyf2-hx9oab
https://wolfram.com/xid/0g7itfcdyf2-cg5jg0
https://wolfram.com/xid/0g7itfcdyf2-pf9xkh
https://wolfram.com/xid/0g7itfcdyf2-zp24k
随机变量的 RootMeanSquare 是 Expectation 的平方根:
https://wolfram.com/xid/0g7itfcdyf2-c5emif
https://wolfram.com/xid/0g7itfcdyf2-cl5rpb
https://wolfram.com/xid/0g7itfcdyf2-ekl2fe
RootMeanSquare 是规模的度量:
https://wolfram.com/xid/0g7itfcdyf2-bhnrki
https://wolfram.com/xid/0g7itfcdyf2-t94no
https://wolfram.com/xid/0g7itfcdyf2-o9323q
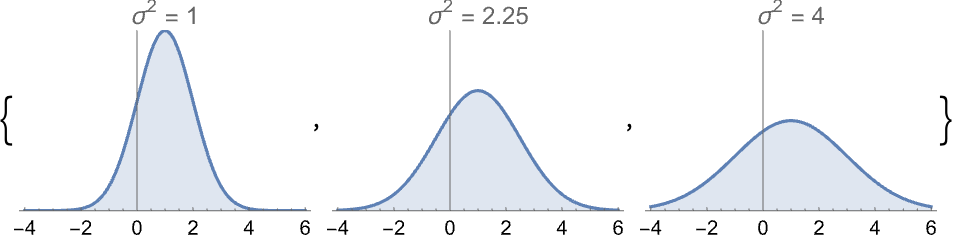
Wolfram Research (2007),RootMeanSquare,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RootMeanSquare.html (更新于 2017 年).文本
Wolfram Research (2007),RootMeanSquare,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RootMeanSquare.html (更新于 2017 年).
Wolfram Research (2007),RootMeanSquare,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RootMeanSquare.html (更新于 2017 年).CMS
Wolfram 语言. 2007. "RootMeanSquare." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.
Wolfram 语言. 2007. "RootMeanSquare." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/RootMeanSquare.html.APA
Wolfram 语言. (2007). RootMeanSquare. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RootMeanSquare.html 年
Wolfram 语言. (2007). RootMeanSquare. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RootMeanSquare.html 年BibTeX
@misc{reference.wolfram_2025_rootmeansquare, author="Wolfram Research", title="{RootMeanSquare}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RootMeanSquare.html}", note=[Accessed: 13-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_rootmeansquare, organization={Wolfram Research}, title={RootMeanSquare}, year={2017}, url={https://reference.wolfram.com/language/ref/RootMeanSquare.html}, note=[Accessed: 13-April-2025
]}