Kurtosis

Kurtosis[data]

gives the coefficient of kurtosis for the elements in data.

Kurtosis[dist]

gives the coefficient of kurtosis for the distribution dist.

Details

Kurtosis measures the concentration of data around the peak and in the tails versus the concentration in the flanks.
Kurtosis[…] is equivalent to CentralMoment[…,4]/CentralMoment[…,2]².
A normal distribution has kurtosis 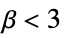equal to 3. In comparing shapes with normal we have:
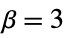
more flat than normal, platykurtic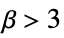

like normal, mesokurtic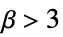

more peaked than normal, leptokurtic

Kurtosis[{{x₁,y₁,…},{x₂,y₂,…},…}] gives {Kurtosis[{x₁,x₂,…}],Kurtosis[{y₁,y₂,…}],…}.
Kurtosis handles both numerical and symbolic data.
The data can have the following additional forms and interpretations:

	Association	the values (the keys are ignored) »
	SparseArray	as an array, equivalent to Normal[data] »
	QuantityArray	quantities as an array »
	WeightedData	weighted mean, based on the underlying EmpiricalDistribution »
	EventData	based on the underlying SurvivalDistribution »
	TimeSeries, TemporalData, …	vector or array of values (the time stamps ignored) »
	Image,Image3D	RGB channel's values or grayscale intensity value »
	Audio	amplitude values of all channels »

For a random process proc, the kurtosis function can be computed for slice distribution at time t, SliceDistribution[proc,t], as β[t]=Kurtosis[SliceDistribution[proc,t]]. »

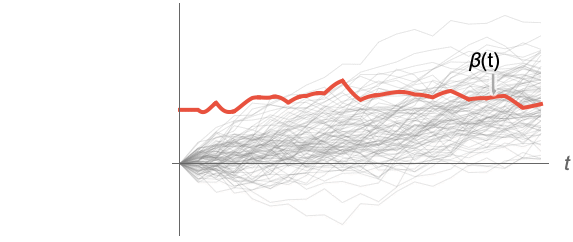
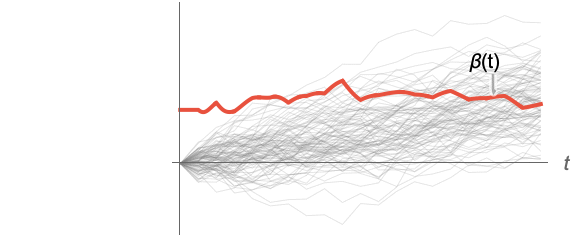
Examples

open allclose all

Basic Examples (2)

Kurtosis for a list of values:

Kurtosis for a symbolic data:

Kurtosis for a parametric distribution:

Scope (18)

Basic Uses (7)

Exact input yields exact output:

Approximate input yields approximate output:

Find the kurtosis of WeightedData:

Find the kurtosis of EventData:

Find the kurtosis of TemporalData:

Find the kurtosis of TimeSeries:

The kurtosis depends only on the values:

Find the kurtosis of data involving quantities:

Array Data (5)

Kurtosis for a matrix gives columnwise kurtosis:

Work with large arrays:

When the input is an Association, Kurtosis works on its values:

SparseArray data can be used just like dense arrays:

Find the kurtosis of a QuantityArray:

Image and Audio Data (2)

Channelwise kurtosis value of an RGB image:

Mean intensity value of a grayscale image:

On audio objects, Kurtosis works channelwise:

Distributions and Processes (4)

Find the kurtosis for univariate distributions:

Multivariate distributions:

Kurtosis for derived distributions:

Data distribution:

Kurtosis for distributions with quantities:

Kurtosis function for a random process:

Applications (6)

Normal distributions have Kurtosis value 3:

Leptokurtic distributions have kurtosis greater than 3:

Platykurtic distributions have kurtosis less than 3:

The limiting distribution for BinomialDistribution as is normal:

The limiting value of the kurtosis is 3:

By the central limit theorem, kurtosis of normalized sums of random variables will converge to 3:

Define a Pearson distribution with zero mean and unit variance, parameterized by skewness and kurtosis:

Obtain parameter inequalities for Pearson types 1, 4, and 6:

The region plot for Pearson types depending on the values of skewness and kurtosis:

Generate a random sample from a ParetoDistribution:

Determine the type of PearsonDistribution with moments matching the sample moments:

This time series contains the number of steps taken daily by a person during a period of five months:

Average number of steps:

Analyze the kurtosis as an indication of consistency of daily steps taken:

The histogram of the frequency of daily counts shows that distribution is mesokurtic:

Find the skewness for the heights of the children in a class:

Kurtosis larger than 3 would indicate a distribution highly concentrated around the mean:

Properties & Relations (5)

Kurtosis for data can be computed from CentralMoment:

Kurtosis for a distribution can be computed from CentralMoment:

Kurtosis is bounded from below by 1, as $TemplateBox[{4}, CentralMoment]⩵Expectation[(x-mu)^4]>=Expectation[(x-mu)^2]^2⩵TemplateBox[{2}, CentralMoment]^2$ :

Normal distributions have Kurtosis value 3:

Approximately normal distributions have Kurtosis values near 3:

Plot the PDF for the distribution:

Plot the PDF for the normal approximation:

Possible Issues (2)

Kurtosis coefficient is sometimes confused with excess kurtosis coefficient:

The excess kurtosis vanishes for NormalDistribution:

Excess kurtosis is defined as Cumulant[dist,4]/Cumulant[dist,2]^2:

Kurtosis may be undefined for data:

Kurtosis may be undefined for a distribution:

Neat Examples (1)

The distribution of Kurtosis estimates for 20, 100, and 300 samples:

Top

Kurtosis

Details

Examples

Basic Examples (2)