- See Also
-
Related Guides
- Normal and Related Distributions
- Probability & Statistics
- Random Variables
- Probability & Statistics with Quantities
- Mathematical Functions
- Numbers with Uncertainty
- Scientific Models
- Parametric Statistical Distributions
- Functions Used in Statistics
- Actuarial Computation
- Distributions in Communication Systems
- Tech Notes
-
- See Also
-
Related Guides
- Normal and Related Distributions
- Probability & Statistics
- Random Variables
- Probability & Statistics with Quantities
- Mathematical Functions
- Numbers with Uncertainty
- Scientific Models
- Parametric Statistical Distributions
- Functions Used in Statistics
- Actuarial Computation
- Distributions in Communication Systems
- Tech Notes
NormalDistribution[μ,σ]
represents a normal (Gaussian) distribution with mean μ and standard deviation σ.
represents a normal distribution with zero mean and unit standard deviation.


NormalDistribution
NormalDistribution[μ,σ]
represents a normal (Gaussian) distribution with mean μ and standard deviation σ.
represents a normal distribution with zero mean and unit standard deviation.
Details
- The probability density for value
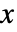 in a normal distribution is proportional to
in a normal distribution is proportional to 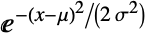 . »
. » - NormalDistribution allows μ to be any real number and σ to be any positive real number.
- NormalDistribution allows μ and σ to be any quantities of the same unit dimensions. »
- NormalDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- NormalDistribution[μ,σ] represents the so-called "normal" statistical distribution that is defined over the real numbers. The distribution is parametrized by a real number μ and a positive real number σ, where μ is the mean of the distribution, σ is known as the standard deviation, and σ2 is known as the variance. The probability density function (PDF) of a normal distribution is unimodal, with the peak occurring at the mean
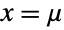 , and the parameter σ determines both the height of the PDF and the "thickness" of its tails. The PDF of a normal distribution is symmetric about its maximum, and the tails of its PDF are "thin" in the sense that the PDF decreases exponentially for large values of
, and the parameter σ determines both the height of the PDF and the "thickness" of its tails. The PDF of a normal distribution is symmetric about its maximum, and the tails of its PDF are "thin" in the sense that the PDF decreases exponentially for large values of 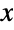 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The zero-argument form NormalDistribution[] is equivalent to NormalDistribution[0,1] and is sometimes called the standard normal distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The zero-argument form NormalDistribution[] is equivalent to NormalDistribution[0,1] and is sometimes called the standard normal distribution. - Due to the presence of the Gaussian function
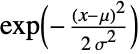 in its PDF, a normal distribution is sometimes referred to as a Gaussian distribution. Informally, a normal distribution may also be referred to as a "bell curve" as a result of the bell-like shape of its PDF. However, it should be noted that other distributions such as CauchyDistribution, StudentTDistribution, and LogisticDistribution also display qualitatively similar "bell" shapes.
in its PDF, a normal distribution is sometimes referred to as a Gaussian distribution. Informally, a normal distribution may also be referred to as a "bell curve" as a result of the bell-like shape of its PDF. However, it should be noted that other distributions such as CauchyDistribution, StudentTDistribution, and LogisticDistribution also display qualitatively similar "bell" shapes. - Random variables that are normally distributed are sometimes called normal variates, and the standard normal distribution may also be referred to as the unit normal distribution.
- Normal distributions are among the most widely occurring probability distributions and thus have many applications. For example, normally distributed values are of fundamental importance in applications of the Monte Carlo method. In addition, the normal distribution is also fundamental in defining the so-called Wiener process, a continuous-time stochastic process
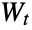 consisting of independent increments
consisting of independent increments 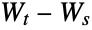 , each of which is independent and identically normally distributed with
, each of which is independent and identically normally distributed with 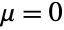 and
and 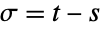 for
for 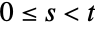 . Moreover, a number of probabilistic and statistical values including percentile ranks and
. Moreover, a number of probabilistic and statistical values including percentile ranks and 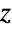 - and
- and 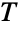 -scores are derived from normal distributions. Furthermore, because of the central limit theorem, the mean of a sufficiently large number of independent random variables will be approximately normally distributed provided certain hypotheses are satisfied, regardless of the original distributions describing the variables. The normal distribution also arises naturally when modeling a number of physical phenomena, such as the velocity of ideal gas molecules, the positions of particles experiencing diffusion, and the long-timescale behavior of thermal light. In addition, a large number of biological phenomena, including sizes of living tissue and quantities such as fasting blood glucose level and blood pressure, yield variables whose logarithms tend to be normally distributed.
-scores are derived from normal distributions. Furthermore, because of the central limit theorem, the mean of a sufficiently large number of independent random variables will be approximately normally distributed provided certain hypotheses are satisfied, regardless of the original distributions describing the variables. The normal distribution also arises naturally when modeling a number of physical phenomena, such as the velocity of ideal gas molecules, the positions of particles experiencing diffusion, and the long-timescale behavior of thermal light. In addition, a large number of biological phenomena, including sizes of living tissue and quantities such as fasting blood glucose level and blood pressure, yield variables whose logarithms tend to be normally distributed. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a normal distribution. Distributed[x,NormalDistribution[μ,σ]], written more concisely as xNormalDistribution[μ,σ], can be used to assert that a random variable x is distributed according to a normal distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[NormalDistribution[μ,σ],x] and CDF[NormalDistribution[μ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a normal distribution, EstimatedDistribution to estimate a normal parametric distribution from given data, and FindDistributionParameters to fit data to a normal distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic normal distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic normal distribution.
- TransformedDistribution can be used to represent a transformed normal distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a normal distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving normal distributions.
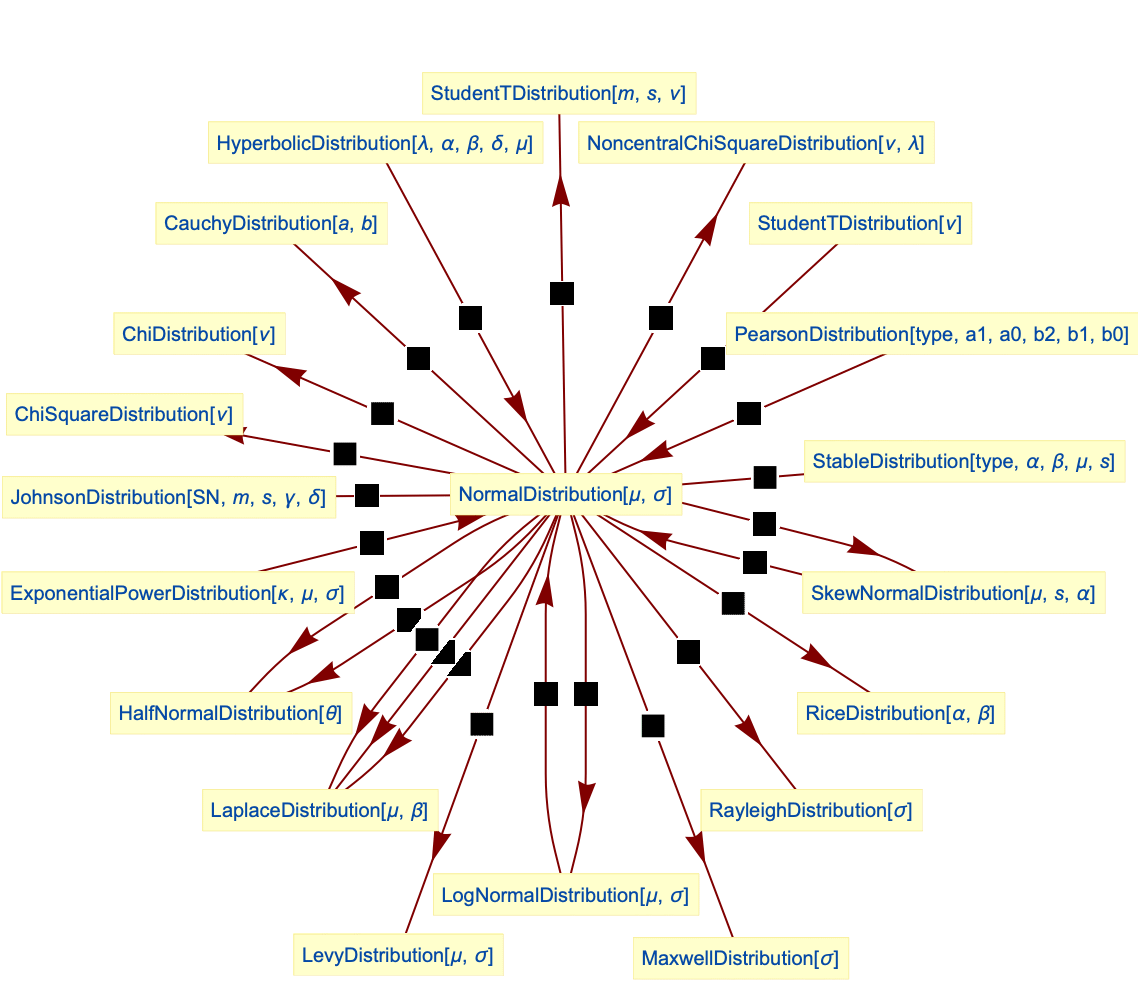
- NormalDistribution is closely related to a number of other distributions. A number of distributions, including LogNormalDistribution, HalfNormalDistribution, NoncentralChiSquareDistribution, and LevyDistribution, can be viewed as transformed versions of NormalDistribution, while NormalDistribution can also be considered a limiting case of a number of distributions, including HyperbolicDistribution, StudentTDistribution, PoissonDistribution, and BinomialDistribution. In addition, NormalDistribution is a special case of ExponentialPowerDistribution (PDF[NormalDistribution[μ,σ],x] is the same as PDF[ExponentialPowerDistribution[2,μ,σ],x]), SkewNormalDistribution (PDF[NormalDistribution[μ,σ],x] is the same as PDF[SkewNormalDistribution[μ,σ,0],x]), and PearsonDistribution (PDF[NormalDistribution[μ,σ],x] is the same as PDF[PearsonDistribution[3,σ-2,-μ σ-2,0,0,1],x] when σ>0) and is the marginal distribution of BinormalDistribution and MultinormalDistribution. NormalDistribution is also closely related to StableDistribution, RiceDistribution, RayleighDistribution, MaxwellDistribution, LevyDistribution, LaplaceDistribution, JohnsonDistribution, ChiDistribution, and ChiSquareDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from a normal distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Hazard function of a normal distribution is increasing:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (11)
Find the percentage of values that lie between ![]() and
and ![]() :
:
Compute ![]() ‐values for a
‐values for a ![]() ‐test under the null hypothesis
‐test under the null hypothesis ![]() and the alternative
and the alternative ![]() :
:
A battery has a lifetime that is approximately normally distributed with a mean of 1000 hours and a standard deviation of 50 hours. Find the fraction with a lifetime between 800 and 1000 hours:
Out of 100 batteries, compute how many have a lifetime between 800 and 1000 hours:
Coffee beans are sold in 5 lb sacks that have true weight normally distributed with a mean of 5 lbs and a variance of 0.01 lb![]() . Find the probability that a given sack weighs at least 4 lbs, 15 oz:
. Find the probability that a given sack weighs at least 4 lbs, 15 oz:
This can be directly computed from the SurvivalFunction:
A company manufactures nails with length normally distributed, mean 0.497 inches, and standard deviation 0.002 inches. Find the fraction that satisfies the specification of length equal to 0.5 inches plus/minus 0.004 inches:
Direct computation with CDF:
A company manufactures nails with length normally distributed and a mean of 0.5 inches. If 50% of the produced nails have lengths between 0.495 and 0.505, find the standard deviation:
A sample is selected from a distribution with mean 5 and standard deviation 1.5. Find the minimum size ![]() of the sample so that with probability 0.97 the sample mean is within 0.8 of the distribution mean:
of the sample so that with probability 0.97 the sample mean is within 0.8 of the distribution mean:
The probability as a function of sample size:
Find the minimum sample size ![]() :
:
The weight of a person, including luggage, has normal distribution with mean 225 lbs and standard deviation 50 lbs. A plane's load limit is 10000 lbs and it can take 44 passengers. With the maximum number of passengers on board, find the probability of the plane being overloaded:
Normally distributed points in the plane:
Normally distributed points in 3D:
Normal distribution was traditionally used to analyze the fractional stock price changes from the previous closing price. Find the estimated distribution for the daily fractional price changes of the S&P 500 index from January 1, 2000, to January 1, 2009:
The range of fractional prices falls within the range of the normal distribution:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the probability of the fractional price change being greater than 0.5%:
Find the mean fractional price change:
Simulate fractional price changes for 30 days:
Show that using LogisticDistribution provides better fit than using normal distribution:
Properties & Relations (36)
Normal distribution is closed under translation and scaling:
In general, affine transformations of independent normals are normal:
Normal distribution is closed under addition:
The normal distribution is symmetric about its mean:
Parameter mixture of a normal distribution with a normal distribution is again a normal distribution:
Relationships to other distributions:
Normal (SN) JohnsonDistribution is a normal distribution:
StudentTDistribution goes to a normal distribution as ![]() goes to
goes to ![]() :
:
Normal distribution is a transformation of LogNormalDistribution:
The inverse transformation of normal distribution yields LogNormalDistribution:
HalfNormalDistribution is a truncated normal distribution:
The normal and half-normal distributions:
HalfNormalDistribution is a transformation of normal distribution:
HalfNormalDistribution is a transformation of normal distribution:
NormalDistribution is a special case of ExponentialPowerDistribution:
Normal distribution is a special case of SkewNormalDistribution with shape parameter ![]() :
:
SkewNormalDistribution is a transformation of normal distribution:
Sum of squares of ![]() standard normally distributed variables follows ChiSquareDistribution:
standard normally distributed variables follows ChiSquareDistribution:
Sum of squares of normally distributed variables has NoncentralChiSquareDistribution:
The norm of ![]() standard normally distributed variables follows ChiDistribution:
standard normally distributed variables follows ChiDistribution:
The norm of three standard normal variables has MaxwellDistribution, a case of ChiDistribution:
The norm of two standard normally distributed variables follows RayleighDistribution:
The norm of two normally distributed variables follows RiceDistribution:
NormalDistribution is the limiting case of HyperbolicDistribution of ![]() for
for ![]() and
and ![]() :
:
If ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are independent and normal, then
are independent and normal, then ![]() has LaplaceDistribution:
has LaplaceDistribution:
Confirm via equality of CharacteristicFunction:
If ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are independent and normal, then
are independent and normal, then ![]() has LaplaceDistribution:
has LaplaceDistribution:
Confirm via equality of CharacteristicFunction:
Ratio of two normally distributed variables has CauchyDistribution:
Square of a normally distributed variable is a special case of GammaDistribution, and also of ChiSquareDistribution:
LaplaceDistribution is a parameter mixture of a normal distribution with RayleighDistribution:
StudentTDistribution is a parameter mixture of a normal distribution with GammaDistribution:
LevyDistribution is a transformation of a normal distribution:
Normal distribution is a special case of type 3 PearsonDistribution:
Normal distribution is a StableDistribution:
Normal distribution is the marginal distribution of BinormalDistribution:
Normal distribution is the marginal distribution of MultinormalDistribution:
NormalDistribution can be obtained from MultinormalDistribution:
StudentTDistribution can be obtained from NormalDistribution and ChiSquareDistribution:
NoncentralStudentTDistribution can be obtained from NormalDistribution and ChiSquareDistribution:
VarianceGammaDistribution can be obtained from GammaDistribution and normal distribution:
Possible Issues (2)
NormalDistribution is not defined when μ is not a real number:
NormalDistribution is not defined when σ is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
StudentTDistribution ChiDistribution ChiSquareDistribution MaxwellDistribution RayleighDistribution RiceDistribution HalfNormalDistribution SkewNormalDistribution BinormalDistribution MultinormalDistribution Erf InverseErf GaussianMatrix Around
Function Repository: NormalCI SigmaConfidenceLevel
Tech Notes
Related Guides
-
▪
- Normal and Related Distributions ▪
- Probability & Statistics ▪
- Random Variables ▪
- Probability & Statistics with Quantities ▪
- Mathematical Functions ▪
- Numbers with Uncertainty ▪
- Scientific Models ▪
- Parametric Statistical Distributions ▪
- Functions Used in Statistics ▪
- Actuarial Computation ▪
- Distributions in Communication Systems
Text
Wolfram Research (2007), NormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/NormalDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "NormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NormalDistribution.html.
APA
Wolfram Language. (2007). NormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NormalDistribution.html
BibTeX
@misc{reference.wolfram_2025_normaldistribution, author="Wolfram Research", title="{NormalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/NormalDistribution.html}", note=[Accessed: 22-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_normaldistribution, organization={Wolfram Research}, title={NormalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/NormalDistribution.html}, note=[Accessed: 22-January-2026]}