LevyDistribution[μ,σ]
represents a Lévy distribution with location parameter μ and dispersion parameter σ.


LevyDistribution
LevyDistribution[μ,σ]
represents a Lévy distribution with location parameter μ and dispersion parameter σ.
Details
- The probability density for value
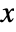 in a Lévy distribution is proportional to
in a Lévy distribution is proportional to 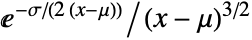 . »
. » - The Lévy distribution LevyDistribution[0,σ] is a special case of the inverse gamma distribution with
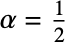 and
and 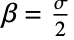 . »
. » - LevyDistribution allows μ to be any real number and σ to be any positive real number.
- LevyDistribution allows μ and σ to be any quantities of the same unit dimensions. »
- LevyDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- LevyDistribution[μ,σ] represents a statistical distribution supported on the interval
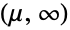 and parametrized by a real number μ (called a "location parameter") and by a positive real number σ (called a "dispersion parameter"). Overall, the probability density function (PDF) of a Lévy distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its concentration near the line
and parametrized by a real number μ (called a "location parameter") and by a positive real number σ (called a "dispersion parameter"). Overall, the probability density function (PDF) of a Lévy distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its concentration near the line 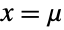 , and the horizontal location of its maximum) is determined by the values of μ and σ. In addition, the tails of the PDF are "fat" in the sense that the PDF decreases algebraically rather than exponentially for large values of
, and the horizontal location of its maximum) is determined by the values of μ and σ. In addition, the tails of the PDF are "fat" in the sense that the PDF decreases algebraically rather than exponentially for large values of 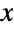 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Lévy distribution is a so-called stable distribution (StableDistribution) in the sense that any linear combination of independent Lévy-distributed random variables is again Lévy-distributed, and should not be confused with the more general terms "Pareto–Lévy distribution" and "Lévy (α)-stable distribution", which are used to describe certain subsets of stable distributions.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Lévy distribution is a so-called stable distribution (StableDistribution) in the sense that any linear combination of independent Lévy-distributed random variables is again Lévy-distributed, and should not be confused with the more general terms "Pareto–Lévy distribution" and "Lévy (α)-stable distribution", which are used to describe certain subsets of stable distributions. - The Lévy distribution is named for French mathematician Paul Lévy, and while one can hardly separate the history of the Lévy distribution from that of the more general class of stable distributions (which were first thoroughly exposited by Lévy in the 1920s), a simplified version of the Lévy distribution PDF was first written about by Danish astronomer Holtsmark in 1919 as part of an investigation of the random fluctuations of gravitational fields. Despite initially being dismissed by mathematicians and probabilists for its apparent lack of real-world applicability, the family of stable distributions has since been employed in the analysis of a wide array of concepts including Brownian motion (cf. the so-called Lévy flight) and is now a fundamental tool in the fields of financial engineering and mathematical finance. In addition, the Lévy distribution has also been used to describe a number of important phenomena in areas such as geomagnetism, particle physics, cryptography, signal analysis, and biology.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Lévy distribution. Distributed[x,LevyDistribution[μ,σ]], written more concisely as xLevyDistribution[μ,σ], can be used to assert that a random variable x is distributed according to a Lévy distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Lévy distributions may be given using PDF[LevyDistribution[μ,σ],x] and CDF[LevyDistribution[μ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively, though because of its long tails, the
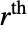 raw and central moments (including the mean and variance) of LevyDistribution are
raw and central moments (including the mean and variance) of LevyDistribution are 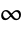 for all
for all 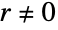 and its moment-generating function (MomentGeneratingFunction) is Indeterminate.
and its moment-generating function (MomentGeneratingFunction) is Indeterminate. - DistributionFitTest can be used to test if a given dataset is consistent with a Lévy distribution, EstimatedDistribution to estimate a Lévy parametric distribution from given data, and FindDistributionParameters to fit data to a Lévy distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Lévy distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Lévy distribution.
- TransformedDistribution can be used to represent a transformed Lévy distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Lévy distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Lévy distributions.
- LevyDistribution is closely related to a number of other distributions. For example, LevyDistribution is an example of StableDistribution (LevyDistribution[μ,σ] is precisely StableDistribution[0,1/2,1,μ+σ,σ]) and hence is related to other stable distributions such as CauchyDistribution, LandauDistribution, and NormalDistribution. LevyDistribution is a special case of both InverseGammaDistribution and PearsonDistribution, and can be obtained as a transformation (via TransformedDistribution) of NormalDistribution. LevyDistribution is also related to HalfNormalDistribution, ChiSquareDistribution, GammaDistribution, and InverseGaussianDistribution.
Examples
open all close allBasic Examples (4)
Scope (6)
Generate a sample of pseudorandom numbers from a Lévy distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Moments of order ![]() do not exist:
do not exist:
Generalized moments exist for order ![]() :
:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
Properties & Relations (7)
Lévy distribution is closed under translation and scaling by a positive factor:
Lévy distribution is closed under addition:
Relationships to other distributions:
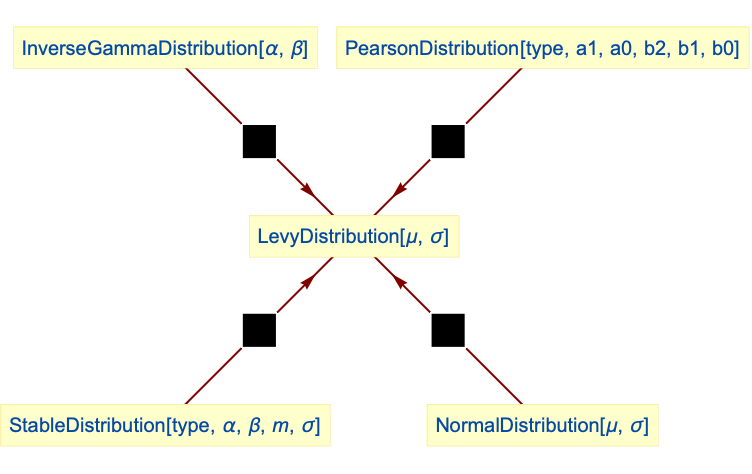
LevyDistribution[0,σ] is a special case of InverseGammaDistribution:
Lévy distribution is a special case of type 5 PearsonDistribution:
Lévy distribution is a transformation of a NormalDistribution:
Lévy distribution is a StableDistribution:
Possible Issues (2)
LevyDistribution is not defined when μ is not a real number:
LevyDistribution is not defined when σ is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Related Guides
Text
Wolfram Research (2008), LevyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LevyDistribution.html (updated 2016).
CMS
Wolfram Language. 2008. "LevyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LevyDistribution.html.
APA
Wolfram Language. (2008). LevyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LevyDistribution.html
BibTeX
@misc{reference.wolfram_2025_levydistribution, author="Wolfram Research", title="{LevyDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/LevyDistribution.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_levydistribution, organization={Wolfram Research}, title={LevyDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/LevyDistribution.html}, note=[Accessed: 25-January-2026]}