WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

InverseGammaDistribution
✖
InverseGammaDistribution

✖

represents an inverse gamma distribution with shape parameter α and scale parameter β.

✖

represents a generalized inverse gamma distribution with shape parameters α and γ, scale parameter β, and location parameter μ.

Details

Background & Context

  • InverseGammaDistribution[α,β,γ,μ] represents a continuous statistical distribution defined over the interval 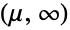and parametrized by a real number μ (called a "location parameter"), two positive real numbers α and γ (called "shape parameters"), and a positive real number β (called a "scale parameter"). Overall, the probability density function (PDF) of an inverse gamma distribution is unimodal with a single "peak" (i.e. a global maximum), with the parameter μ determining the horizontal location of the PDF and the parameters α, β, and γ determining its overall shape (its height, its spread, and its concentration near the 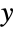axis). In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than decreasing algebraically for large values of 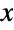. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The four-parameter version is sometimes referred to as the generalized inverse gamma distribution, while the two-parameter form InverseGammaDistribution[α,β] (which is equivalent to InverseGammaDistribution[α,β,1,0]) is often referred to as "the" inverse gamma distribution.
  • InverseGammaDistribution[α,β,γ,μ] is the distribution followed by the reciprocal of a generalized gamma-distributed random variable. In other words, if 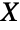is a random variable and XGammaDistribution[α,β,γ,μ] (where denotes "is distributed as"), then 1/XInverseGammaDistribution[α,β,γ,μ]. In Bayesian probability, the inverse gamma distribution is used as a marginal posterior or as a conjugate prior distribution in inferencing of normally-distributed data whose variance is unknown if an uninformative prior or if an informative prior is used, respectively. The inverse gamma distribution and its generalization are also used in other miscellaneous Bayesian applications in addition to being used as tools of study in various areas including reliability theory, manufacturing systems, machine learning, and survival analysis.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an inverse gamma distribution. Distributed[x,InverseGammaDistribution[α,β,γ,μ]], written more concisely as xInverseGammaDistribution[α,β,γ,μ], can be used to assert that a random variable x is distributed according to an inverse gamma distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for inverse gamma distributions may be given using PDF[InverseGammaDistribution[α,β,γ,μ],x] and CDF[InverseGammaDistribution[α,β,γ,μ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with an inverse gamma distribution, EstimatedDistribution to estimate an inverse gamma parametric distribution from given data, and FindDistributionParameters to fit data to an inverse gamma distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic inverse gamma distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic inverse gamma distribution.
  • TransformedDistribution can be used to represent a transformed inverse gamma distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an inverse gamma distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving inverse gamma distributions.
  • InverseGammaDistribution is closely related to a number of other distributions. For example, InverseGammaDistribution is related to InverseChiSquareDistribution (and hence to ChiSquareDistribution) in that the PDF of InverseGammaDistribution[ν/2,1/2] is precisely the same as InverseChiSquareDistribution[ν,1/ν]. InverseGammaDistribution is generalized by PearsonDistribution, generalizes LevyDistribution, and is closely related to a number of other distributions including MoyalDistribution, LogGammaDistribution, ErlangDistribution, BetaDistribution, ExpGammaDistribution, RayleighDistribution, ChiDistribution, WeibullDistribution, and StudentTDistribution.

Examples

open allclose all

Basic Examples  (8)Summary of the most common use cases

Probability density function:

In[6]:=6
✖
https://wolfram.com/xid/0e5ax7116x0eqi-kyintk
Out[6]=6
In[10]:=10
✖
https://wolfram.com/xid/0e5ax7116x0eqi-vmro4u
Out[10]=10
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-b5oiw2
Out[3]=3

Cumulative distribution function:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ke60nq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-lkk1qs
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-chkcda
Out[3]=3

Mean and variance:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-wko5m
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ikj8xg
Out[2]=2

Median:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-rh9pfj
Out[1]=1

Probability density function for the generalized inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-q6wfq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-pvs5md
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-qcgvko
Out[3]=3

Cumulative distribution function for the generalized inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-lrrzbj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-3jbb5a
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-b3vaeq
Out[3]=3

Mean and variance of the generalized inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-dp7z47
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-43b89c
Out[2]=2

Median:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-b3ezv6
Out[1]=1

Scope  (10)Survey of the scope of standard use cases

Generate a sample of pseudorandom numbers from an inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-qhtk5j

Compare its histogram to the PDF:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-03mwaz
Out[2]=2

Generate a set of pseudorandom numbers that have generalized inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-j7vis

Compare its histogram to the PDF:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-3054ke
Out[2]=2

Distribution parameters estimation:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-45b7g2

Estimate the distribution parameters from sample data:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-epi747
Out[2]=2

Compare the density histogram of the sample with the PDF of the estimated distribution:

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-f8ui5o
Out[3]=3

Skewness depends only on shape parameter α:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-0vh7dm
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-smp
Out[2]=2

As α gets larger, the distribution becomes more symmetric:

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-bn11lo
Out[3]=3

The generalized case depends on both α and γ:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-l88qv6
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-s5m7me
Out[5]=5

Kurtosis depends only on shape parameter α:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-gmfy2m
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-qke
Out[2]=2

The kurtosis approaches the kurtosis of NormalDistribution[] as α approaches :

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-e30fok
Out[3]=3

The generalized case depends on both α and γ:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ylrdc0
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-hv55ok
Out[5]=5

Different moments with closed forms as functions of parameters:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-js043h

Moment:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-rx074o
Out[2]=2

CentralMoment:

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-pknsqa
Out[3]=3

FactorialMoment:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-zg9ct4
Out[4]=4

Cumulant:

In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-9gzmth
Out[5]=5

Different moments of generalized inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-c77crz

Moment:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-4kmovf
Out[2]=2

CentralMoment:

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-3gj1w5
Out[3]=3

FactorialMoment:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-9dfwj0
Out[4]=4

Cumulant:

In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-hebrtm
Out[5]=5

Hazard function:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-bdk9lp
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-evtj1n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-4ofbxp
Out[3]=3

Hazard function of generalized inverse gamma distribution:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-kpwv1r
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-zy0dw5
Out[5]=5

Quantile function:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-10c13r
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-b8p0kl
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-kztu2d
Out[3]=3

Generalized inverse gamma distribution:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-jbdwfs
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-12mo7l
Out[5]=5

Consistent use of Quantity in parameters yields QuantityDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-de2jsq
Out[1]=1

Find the mean amount:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-cg0pqk
Out[2]=2

Applications  (1)Sample problems that can be solved with this function

The present value of one-dollar stochastic perpetuity when the rate obeys a Wiener process with shift and volatility follows InverseGaussianDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-cmqspc

Find the expected present value:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-dof12u
Out[2]=2

Compute the no‐volatility limit:

In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ehd3vv
Out[3]=3

Compare with the built-in result:

In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-h53p96
Out[4]=4

Find the probability that the present value is smaller than the no‐volatility limit:

In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-fdrd18
Out[5]=5

Compute the probability when r0.06 and σ0.01:

In[6]:=6
✖
https://wolfram.com/xid/0e5ax7116x0eqi-bulzy9
Out[6]=6

Properties & Relations  (8)Properties of the function, and connections to other functions

Inverse gamma distribution is closed under scaling by a positive factor:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ho2od1
Out[1]=1

Generalized inverse gamma distribution is closed under translation and scaling by a positive factor:

In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ftdkt5
Out[2]=2

Relationships to other distributions:

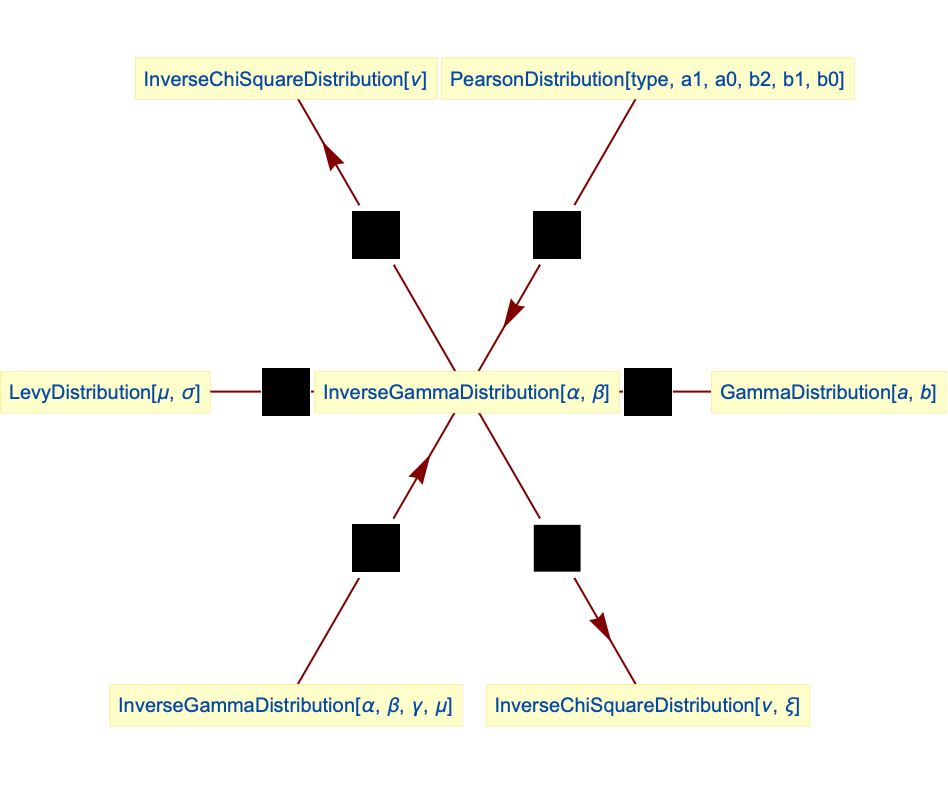
InverseChiSquareDistribution is a special case of inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-vtj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-n5r
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-wx0s82
Out[3]=3

Generalized InverseChiSquareDistribution is a special case of inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-quu160
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-seqztm
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ogd8hd
Out[3]=3

Inverse gamma distribution and GammaDistribution have an inverse relationship:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-h9yioq
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-i14w7i
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-kgxbp5
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0e5ax7116x0eqi-bn4lg5
Out[4]=4

LevyDistribution[0,σ] is a special case of inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-cs8wcv
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-fn8ci7
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-wjw48r
Out[3]=3

Inverse gamma distribution is a special case of type 5 PearsonDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-9hzd6o
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-84oc9z
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-tw3352
Out[3]=3

Generalized inverse gamma distribution simplifies to inverse gamma distribution:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-q1gbn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e5ax7116x0eqi-u889ij
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0e5ax7116x0eqi-51ndsp
Out[3]=3

Possible Issues  (2)Common pitfalls and unexpected behavior

InverseGammaDistribution is not defined when either α or β is not a positive real number:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ebk
Out[1]=1

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-t70
Out[1]=1

Neat Examples  (1)Surprising or curious use cases

PDFs for different β values with CDF contours:

In[1]:=1
✖
https://wolfram.com/xid/0e5ax7116x0eqi-io0104
In[5]:=5
✖
https://wolfram.com/xid/0e5ax7116x0eqi-ceikus
Out[5]=5
Wolfram Research (2008), InverseGammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseGammaDistribution.html (updated 2016).
✖
Wolfram Research (2008), InverseGammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseGammaDistribution.html (updated 2016).

Text

Wolfram Research (2008), InverseGammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseGammaDistribution.html (updated 2016).

✖
Wolfram Research (2008), InverseGammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseGammaDistribution.html (updated 2016).

CMS

Wolfram Language. 2008. "InverseGammaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InverseGammaDistribution.html.

✖
Wolfram Language. 2008. "InverseGammaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InverseGammaDistribution.html.

APA

Wolfram Language. (2008). InverseGammaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseGammaDistribution.html

✖
Wolfram Language. (2008). InverseGammaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseGammaDistribution.html

BibTeX

@misc{reference.wolfram_2025_inversegammadistribution, author="Wolfram Research", title="{InverseGammaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InverseGammaDistribution.html}", note=[Accessed: 16-April-2025 ]}

✖
@misc{reference.wolfram_2025_inversegammadistribution, author="Wolfram Research", title="{InverseGammaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InverseGammaDistribution.html}", note=[Accessed: 16-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inversegammadistribution, organization={Wolfram Research}, title={InverseGammaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/InverseGammaDistribution.html}, note=[Accessed: 16-April-2025 ]}

✖
@online{reference.wolfram_2025_inversegammadistribution, organization={Wolfram Research}, title={InverseGammaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/InverseGammaDistribution.html}, note=[Accessed: 16-April-2025 ]}