ExpGammaDistribution[κ,θ,μ]
represents an exp-gamma distribution with shape parameter κ, scale parameter θ, and location parameter μ.


ExpGammaDistribution
ExpGammaDistribution[κ,θ,μ]
represents an exp-gamma distribution with shape parameter κ, scale parameter θ, and location parameter μ.
Details
- ExpGammaDistribution is at times confused with LogGammaDistribution.
- ExpGammaDistribution is also known as generalized extreme value distribution.
- The survival function for value
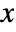 in an exp-gamma distribution is proportional to
in an exp-gamma distribution is proportional to ![TemplateBox[{kappa, {exp, (, {{(, {x, -, mu}, )}, /, theta}, )}}, Gamma2] TemplateBox[{kappa, {exp, (, {{(, {x, -, mu}, )}, /, theta}, )}}, Gamma2]](Files/ExpGammaDistribution.en/2.png) .
. - ExpGammaDistribution allows κ and θ to be any positive real numbers and μ any real number.
- ExpGammaDistribution allows μ and θ to be any quantities with the same unit dimensions, and κ to be a dimensionless quantity. »
- ExpGammaDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- ExpGammaDistribution[κ,θ,μ] represents a continuous statistical distribution defined on the set of real numbers and parametrized by a real number μ, called a "location parameter", and by two positive real numbers κ and θ, called a "shape parameter" and a "scale parameter", respectively. The parameter μ determines the horizontal location of the "peak" (i.e. absolute maximum) of the probability density function (PDF) of the exp-gamma distribution. While the PDF is always unimodal, the overall height and steepness of the graph are determined by the values of κ and θ. In addition, the tails of the PDF are "fat", in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of
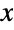 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The term exp-gamma is shorthand for exponential-gamma, and the exp-gamma distribution is sometimes referred to as the generalized extreme value distribution, though caution must be exhibited since that term also collectively refers to a number of qualitatively similar probability distributions.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The term exp-gamma is shorthand for exponential-gamma, and the exp-gamma distribution is sometimes referred to as the generalized extreme value distribution, though caution must be exhibited since that term also collectively refers to a number of qualitatively similar probability distributions. - The exp-gamma distribution is mathematically defined to be the distribution that models
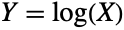 whenever
whenever 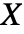 GammaDistribution. Exp-gamma distributions are also significant because of the so-called (statistical) extreme value theorem, which states that the maximum of a sample of independent and identically distributed random variables can only converge in distribution to one of three possible distributions (GumbelDistribution, FrechetDistribution, and WeibullDistribution), all of which are special cases of ExpGammaDistribution. In addition, the exp-gamma distribution has been used in various branches of science to model a number of phenomena, including wind speeds in meteorology and ocean current speeds in ocean engineering.
GammaDistribution. Exp-gamma distributions are also significant because of the so-called (statistical) extreme value theorem, which states that the maximum of a sample of independent and identically distributed random variables can only converge in distribution to one of three possible distributions (GumbelDistribution, FrechetDistribution, and WeibullDistribution), all of which are special cases of ExpGammaDistribution. In addition, the exp-gamma distribution has been used in various branches of science to model a number of phenomena, including wind speeds in meteorology and ocean current speeds in ocean engineering. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an exp-gamma distribution. Distributed[x,ExpGammaDistribution[κ,θ,μ]], written more concisely as xExpGammaDistribution[κ,θ,μ], can be used to assert that a random variable x is distributed according to an exp-gamma distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[ExpGammaDistribution[κ,θ,μ],x] and CDF[ExpGammaDistribution[κ,θ,μ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with an exp-gamma distribution, EstimatedDistribution to estimate an exp-gamma parametric distribution from given data, and FindDistributionParameters to fit data to an exp-gamma distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic exp-gamma distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic exp-gamma distribution.
- TransformedDistribution can be used to represent a transformed exp-gamma distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an exp-gamma distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving exp-gamma distributions.
- The exp-gamma distribution is related to a number of other distributions. By definition, ExpGammaDistribution is a transformation of GammaDistribution, in the sense that the CDF of ExpGammaDistribution[κ,θ,0] is precisely that of θ Log[u], where uGammaDistribution[κ,1]. In addition, a number of distributions, including GumbelDistribution, FrechetDistribution, and WeibullDistribution, fit under the broader heading of "generalized extreme value distributions" and hence are related qualitatively to ExpGammaDistribution, a relationship that can be made quantitative by noting that both FrechetDistribution and GumbelDistribution are transformations of WeibullDistribution and that ExpGammaDistribution[1,b,a] is precisely GumbelDistribution[a,b]. ExpGammaDistribution[1,σ,μ] is the same as MinStableDistribution[μ,σ,0], while MoyalDistribution[μ,σ] can be obtained as the distribution of the random variate -u, where uExpGammaDistribution[1/2,σ,-μ+σ Log[2]]. Exp-gamma is also related to ExtremeValueDistribution, ParetoDistribution, LogisticDistribution, and MaxStableDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from an exp-gamma distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the shape parameter κ:
Kurtosis depends only on the shape parameter κ:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
ExpGammaDistribution can be used to model monthly maximum wind speeds. Recorded monthly maxima of wind speeds in km/h for Boston, MA, from January 1950 till December 2009:
Fit the distribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the probability of monthly maximum wind exceeding 50 mph:
Properties & Relations (6)
Exp-gamma distribution is closed under translation and scaling by a positive factor:
Relationships to other distributions:
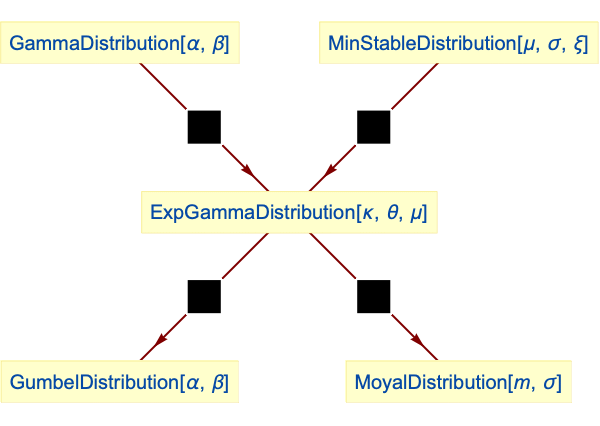
ExpGammaDistribution is a transformation of GammaDistribution:
GumbelDistribution is a special case of ExpGammaDistribution:
ExpGammaDistribution is a special case of MinStableDistribution:
MoyalDistribution is a transformed ExpGammaDistribution:
Related Guides
Text
Wolfram Research (2010), ExpGammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ExpGammaDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "ExpGammaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ExpGammaDistribution.html.
APA
Wolfram Language. (2010). ExpGammaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExpGammaDistribution.html
BibTeX
@misc{reference.wolfram_2025_expgammadistribution, author="Wolfram Research", title="{ExpGammaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ExpGammaDistribution.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_expgammadistribution, organization={Wolfram Research}, title={ExpGammaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ExpGammaDistribution.html}, note=[Accessed: 11-January-2026]}