Log

Log[z]

gives the natural logarithm of z (logarithm to base ).

Log[b,z]

gives the logarithm to base b.

Details

  • Log is a mathematical function, suitable for both symbolic and numerical manipulation.
  • Log gives exact rational number results when possible.
  • For certain special arguments, Log automatically evaluates to exact values.
  • Log can be evaluated to arbitrary numerical precision.
  • Log automatically threads over lists.
  • Log[z] has a branch cut discontinuity in the complex z plane running from 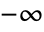to .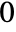
  • Log can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (6)

Log gives the natural logarithm (to base ):

Log[b,z] gives the logarithm to base b:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion shifted from the origin:

Asymptotic expansion at a singular point:

Scope  (51)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate numerically to high precision:

The precision of the output tracks the precision of the input:

Complex arguments:

Evaluate Log efficiently at high precision:

Log threads elementwise over lists and matrices:

It threads over lists in either argument:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix Log function using MatrixFunction:

Specific Values  (5)

Simple exact values are generated automatically:

Values at infinity:

Zero argument gives a symbolic result:

Zero of Log:

Find a value of x for which the Log[x]=0.5:

Visualization  (3)

Plot the Log function:

Plot the real part of :

Plot the imaginary part of :

Polar plot with :

Function Properties  (12)

Log[z] gives the logarithm with base E:

Log is defined for all real positive values:

Complex domain:

Log achieves all real values:

The range for complex values:

Log is the inverse of Exp:

is not an analytic function:

Nor is it meromorphic:

The issue is a branch cut along the negative real axis:

The branch cut exists for any fixed value of :

is increasing on the positive reals for and decreasing for :

Log is injective:

Log is surjective:

Log is neither non-negative nor non-positive:

has both singularities and discontinuities for x≤0:

is concave on the positive reals for and convex for :

TraditionalForm formatting:

Differentiation  (5)

The first derivative with respect to z:

The first derivative with respect to b:

Higher derivatives:

Formula for the ^(th) derivative:

Derivative of a nested logarithmic function:

Integration  (3)

Indefinite integrals of Log:

Definite integral of Log:

More integrals:

Series Expansions  (5)

Taylor expansion for Log:

Plot the first three approximations for Log around :

General term in the series expansion of Log around :

Asymptotic expansions at the branch cut:

The first term in the Fourier series of Log:

Log can be applied to power series:

Function Identities and Simplifications  (6)

Basic identity for Log:

Logarithm of a power function simplification:

Simplify logarithms with assumptions:

Logarithm of a product:

Change of base:

Expand assuming real variables x and y:

Function Representations  (5)

Integral representation:

Series representation:

Log arises from the power function in a limit:

Log can be represented in terms of MeijerG:

Log can be represented as a DifferentialRoot:

Generalizations & Extensions  (2)

Log can deal with real‐valued intervals from :

Log is a numerical function:

Applications  (8)

Plot Log for various bases:

Plot the real and imaginary parts of Log:

Plot the real and imaginary parts over the complex plane:

Plot data logarithmically and doubly logarithmically:

Benford's law predicts that the probability of the first digit is in many sequences:

Analyze the first digits of the following sequence:

Use Tally to count occurrences of each digit:

Shannon entropy for a set of probabilities:

Equi‐entropy surfaces for four symbols:

Approximate the ^(th) prime number:

Exponential divergence of two nearby trajectories for a quadratic map:

Properties & Relations  (13)

Compositions with the inverse function might need PowerExpand:

Get expansion that is correct for all complex arguments:

Simplify logarithms with assumptions:

Convert inverse trigonometric and hyperbolic functions into logarithms:

Log arises from the power function in a limit:

Solve a logarithmic equation:

Reduce a logarithmic equation:

Numerically find a root of a transcendental equation:

The natural logarithms of integers are transcendental:

Integral transforms:

Solve differential equations:

Limits:

Log is automatically returned as a special case for various special functions:

Possible Issues  (7)

For a symbolic base, the base b log evaluates to a quotient of logarithms:

Generically, :

Because intermediate results can be complex, approximate zeros can appear:

Machine-precision inputs can give numerically wrong answers on branch cuts:

Use arbitrary‐precision arithmetic to obtain correct results:

Compositions of logarithms can give functions that are zero almost everywhere:

This function is a differential-algebraic constant:

Logarithmic branch cuts can occur without their corresponding branch point:

The argument of the logarithm never vanishes:

But it can take negative values, so the logarithm has a branch cut:

The kink at marks the appearance of the second sheet:

Logarithmic terms in Puiseux series are considered coefficients inside SeriesData:

In traditional form, parentheses are needed around the argument:

Neat Examples  (6)

Successive integrals of the log function:

Amoeba of a cubic:

Plot the Riemann surface of Log:

Plot Log at integer points:

Calculate Log through an analytically continued summed Taylor series:

Visualize how the value is approached as :

Plot the Riemann surface of Log[Log[z]]:

Wolfram Research (1988), Log, Wolfram Language function, https://reference.wolfram.com/language/ref/Log.html (updated 2021).

Text

Wolfram Research (1988), Log, Wolfram Language function, https://reference.wolfram.com/language/ref/Log.html (updated 2021).

CMS

Wolfram Language. 1988. "Log." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Log.html.

APA

Wolfram Language. (1988). Log. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Log.html

BibTeX

@misc{reference.wolfram_2025_log, author="Wolfram Research", title="{Log}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Log.html}", note=[Accessed: 03-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_log, organization={Wolfram Research}, title={Log}, year={2021}, url={https://reference.wolfram.com/language/ref/Log.html}, note=[Accessed: 03-July-2025 ]}