Around

Around[x,δ]

represents an approximate number or quantity with a value around x and an uncertainty δ.

Around[x,{δ-,δ+}]

represents a number or quantity with a value around x and asymmetric uncertainties δ-, δ+.

Around[dist]

gives an approximate number or quantity around the mean of the distribution dist, with an uncertainty corresponding to the standard deviation of the distribution.

Around[list]

gives an approximate object around the mean of the elements of list and with an uncertainty corresponding to their standard deviation.

Around[s]

gives an approximate object derived from the number, interval or string specification s.

Details

  • Around[x,δ] is typically displayed as x±δ. If δ is very small compared to x, as in Around[1.2345678,0.0000012], it is instead displayed in a form like .
  • Around[x,δ] can be used to represent results of measurements in which there is statistical or other uncertainty.
  • Around[x,Scaled[ϕ]] represents a number with relative error ϕ, corresponding to Around[x,ϕ x].
  • When Around is used in computations, uncertainties are by default propagated using a first-order series approximation, assuming no correlations.
  • Around[…]["prop"] can be used to extract the following properties:
  • "Value"central value x in Around[x,δ]
    "Uncertainty"uncertainty δ in Around[x,δ]
    "Number"number with value x and accuracy corresponding to δ
    "Interval"Interval[{x-δ,x+δ}]
  • In Around[s], numbers with uncertainty can be specified as follows:
  • x (approximate number)Around[x,(10^-Accuracy[x])/2]
    Interval[{xmin,xmax}]Around[(xmax+xmin)/2,(xmax-xmin)/2]
    dist (statistical distribution)Around[Mean[dist],StandardDeviation[dist]]
    list (list of elements)Around[Mean[list],StandardDeviation[list]]
    "nn.dddd" (number string)(uncertainty determined by number of significant digits)
  • For linear computations, Around[x,δ] behaves like a number whose values are distributed according to the normal distribution NormalDistribution[x,δ].
  • Relational operators like Less, Equal and Greater on Around objects Around[x1,δ1] and Around[x2,δ2] return True or False depending on whether the distance between centers x1 and x2 is larger or smaller than 2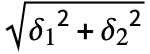. Numbers are assigned zero uncertainty when compared to Around objects.
  • NumericalOrder[Around[x1,δ1],Around[x2,δ2]] returns 0 if the distance between centers x1, x2 is smaller than 0.5. Otherwise it returns 1 or , depending on the ordering of centers. Numbers are assigned zero uncertainty when sorted numerically together with Around objects.
  • In Around[x,δ], the value x and the uncertainty δ can be any numeric or symbolic expressions. If δ is a numeric expression, then both x and δ will be made numerical. By default, machine precision will be used, but higher precision may be used if needed to represent the numbers faithfully.
  • Around[x,δ] displays with one or two digits of the uncertainty δ shown; x is shown with the same number of digits to the right of the decimal point as is shown in δ.
  • In Around[x,δ], x and δ can be quantities with different, though compatible, units.
  • Around[{x1,x2,…},δ] threads over the list in its first argument, effectively treating the uncertainties in the xi as being uncorrelated.

Examples

open allclose all

Basic Examples  (10)

Uncertain numbers of different sizes and uncertainties:

Uncertain Quantity objects with different units:

An Around object with asymmetric uncertainties:

Specify a 5% relative uncertainty in input:

Perform operations with Around objects:

Plot a list of Around objects:

Extract the parts of an Around object:

Two different instances of the same Around object are assumed to be uncorrelated:

Therefore, the resulting uncertainty is smaller than that obtained by multiplication by 2:

Use a symbolic Around object:

Perform operations on it:

Add symbolic Around objects, with uncertainties assumed to be uncorrelated:

Scope  (20)

Uncertain Objects  (6)

Uncertain numbers:

Uncertain numbers with asymmetric uncertainties:

Uncertain Quantity objects:

Use a value and an uncertainty of compatible units:

Use the same units in value and uncertainty:

The result is a single Quantity object with an Around magnitude:

Use asymmetric uncertainties with compatible units:

Values of different sizes for the same uncertainty:

Uncertainties of different sizes for the same value:

An uncertain number with 30% relative uncertainty:

Express the same object using a Quantity percentage:

Use Quantity values of any dimension:

Accessors and Conversions  (4)

Extract the value and uncertainty of an Around object:

Construct a finite precision number from an Around object:

Its accuracy coincides with the uncertainty of a:

Reconstruct the original Around object from the finite-precision number:

Construct an interval centered at the value of an Around object and with a semi-width given by its uncertainty:

Reconstruct the original Around object from the interval:

Use Around to convert strings containing numbers, assuming uncertainty 0.5 in the last significant digit:

Operations with Uncertain Objects  (4)

Basic operations with numbers:

Basic operations with Quantity objects:

Construct a QuantityArray object whose elements are Around objects:

Perform operations, preserving the QuantityArray structure:

Normalize the result:

Basic operations with symbolic Around objects:

Comparisons and Ordering of Uncertain Objects  (6)

Compare two Around objects with far apart centers:

Their distance is significantly larger than zero:

Compare two Around objects with close centers:

Their distance is not significantly larger than zero:

Compare an Around object with a number:

The distance is significantly larger than zero:

Compare Around objects with Quantity centers and uncertainties:

The distance between them is significantly larger than zero:

Order numerically a collection of Around objects and numbers:

Order numerically a collection of velocities:

Convert to a common base unit to compare values directly:

Applications  (3)

Plot data with uncertainty:

Plot exoplanet radius versus mass, including uncertainties in both variables:

Compute the mean value of the masses and radii:

Compare with the mass and radius of the Earth:

Compute the period of oscillation of a pendulum of length, using a value of for Earth's gravity and assuming an uncertainty of one unit in the last significant digit of those quantities:

Properties & Relations  (3)

Square an Around object, using a first-order series approximation:

Perform the corresponding exact computation using TransformedDistribution:

Using a higher-order series expansion gives a better approximation to the exact result:

Using Around directly on the asymmetric distribution returns an object with asymmetric uncertainty:

Take a normal distribution and simulate it:

Around[scalars] estimates the mean and standard deviation of the distribution:

Around[dist] gives the true parameters in the distribution dist:

MeanAround[scalars] describes the mean of the distribution and the standard error of the mean:

Around[x,δ] and CenteredInterval[x,δ] use different propagation rules in numeric operations:

Wolfram Research (2019), Around, Wolfram Language function, https://reference.wolfram.com/language/ref/Around.html (updated 2023).

Text

Wolfram Research (2019), Around, Wolfram Language function, https://reference.wolfram.com/language/ref/Around.html (updated 2023).

CMS

Wolfram Language. 2019. "Around." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/Around.html.

APA

Wolfram Language. (2019). Around. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Around.html

BibTeX

@misc{reference.wolfram_2024_around, author="Wolfram Research", title="{Around}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/Around.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_around, organization={Wolfram Research}, title={Around}, year={2023}, url={https://reference.wolfram.com/language/ref/Around.html}, note=[Accessed: 30-December-2024 ]}