Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

MultiplicativeOrder

MultiplicativeOrder[k,n]

gives the multiplicative order of k modulo n, defined as the smallest integer such that .

MultiplicativeOrder[k,n,{r₁,r₂,…}]

gives the generalized multiplicative order of k modulo n, defined as the smallest integer such that for some .

Details

MultiplicativeOrder is also known as modulo order or haupt‐exponent.
Integer mathematical function, suitable for both symbolic and numerical manipulation.
Typically used in modular arithmetic and cryptography.
MultiplicativeOrder[k,n] gives the smallest positive integer m such that the remainder when dividing k^m by n is equal to 1.
MultiplicativeOrder returns unevaluated if there is no integer 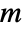satisfying the necessary conditions.

For a FiniteFieldElement object a, MultiplicativeOrder[a] gives the multiplicative order of a, defined as the smallest positive integer m such that 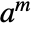is the multiplicative identity of the finite field.

Examples

open allclose all

Basic Examples (2)

The multiplicative order of 5 modulo 8:

Plot the sequence with a fixed modulus:

Plot the sequence, varying the modulus:

Scope (7)

Numerical Evaluation (5)

Compute using integers:

Generalized multiplicative order:

Compute using large numbers:

Multiplicative order of finite field elements:

TraditionalForm formatting:

Symbolic Manipulation (2)

Use Solve to find solutions of equations:

Use FindInstance to find solutions:

Applications (9)

Basic Applications (5)

Find all primitive roots modulo 43:

A rational number has a digit cycle of length if is prime and 10 is a primitive root for :

Compute MultiplicativeOrder using NestWhileList:

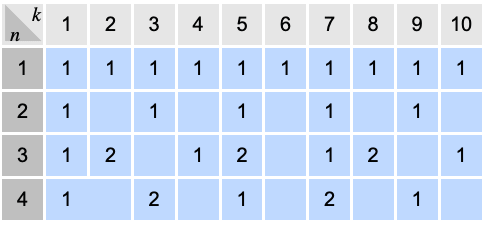
Count number of possible multiplicative orders modulo a given prime number:

The number of divisors of where is prime:

These are in fact the same list:

Number Theory (4)

The repetition period in Rule for odd divides q[n]:

The digits of in base repeat with period :

The function digitCycleLength gives the digit period for any rational number in base :

This shows that the decimal representation of in base 10 repeats every 3 digits:

Build an RSA-like toy encryption scheme:

Perform a cycling attack. One of the outputs will be the plaintext:

Properties & Relations (5)

The multiplicative order of a primitive root modulo n is EulerPhi[n]:

EulerPhi divides MultiplicativeOrder:

The result is always positive:

Find the smallest integer such that ≡ 2, 3, or 4 mod 7:

Find which of the remainders satisfies :

Solve the discrete log problem with :

Possible Issues (1)

For nonzero integers k and n, MultiplicativeOrder[k,n] exists if and only if k and n are coprime:

However, 10 and 22 are not coprime:

Interactive Examples (1)

MultiplicativeOrder of each integer below a given prime number:

Neat Examples (2)

Visualize when a number has multiplicative order modulo 12:

Ulam spiral of MultiplicativeOrder:

Top