Details

The degree n of CyclicGroup[n] must be a non-negative integer. Degrees 0 and 1 correspond to the trivial or identity group.
CyclicGroup[n] is represented by default as a permutation group on the points {1,…,n}.
Cyclic groups are commutative.

Background & Context

CyclicGroup[n] represents the cyclic group 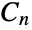of order n (also denoted 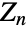, , 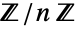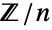or 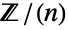) for a given non-negative integer n. For 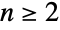, the default representation of CyclicGroup[n] is as a permutation group on the symbols . The special cases CyclicGroup[0] and CyclicGroup[1] are equivalent to the trivial group with exactly one element.
Mathematically, a cyclic group is a group 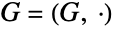containing an element 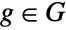known as a generator, such that every element 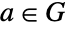can be written in the form 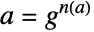for some non-negative integer 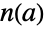less than the order of 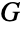. It follows immediately that any such 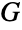is Abelian (i.e. commutative), since 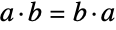for all elements 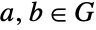. If 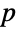is a prime number, any group with 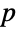elements is isomorphic to CyclicGroup[p], and by the fundamental theorem of finite Abelian groups, every Abelian group 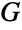having a finite number of elements can be expressed as a direct product 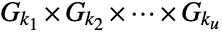, where G_{k_i}=CyclicGroup[k_i] and each k_i is a power of a prime number. Cyclic groups are permutation groups.
The usual group theoretic functions may be applied to CyclicGroup[n], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the cyclic group 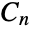are available via FiniteGroupData[{"CyclicGroup",n},"prop"].
The class of cyclic groups serves as the basis for a number of related generalizations including virtually cyclic groups, locally cyclic groups and polycyclic groups, many of which are of fundamental importance in abstract algebra, number theory, geometric group theory and topology.
Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AbelianGroup, AlternatingGroup, DihedralGroup and SymmetricGroup.