Permutation Groups

Generating SetsExample: The Rubik Group
Orbits and StabilizersOther Examples
Strong Generating Set Representation
Groups admit many different representations. In particular, all finite groups can be represented as permutation groups, that is, they are always isomorphic to a subgroup of the symmetric group 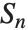of automorphisms of a set of 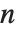elements (Cayley's theorem). Highly efficient techniques for manipulation of permutation groups have been developed during the last 40 years, which allow the manipulation of very large groups in a computer.
The Wolfram Language provides a collection of commands and algorithms that can handle permutation groups of moderate degree, in the range of a few thousand, hence working with groups of permutations with more than elements.
This tutorial introduces some basic algorithms for computing with finite permutation groups, specified by a list of generating permutations given in disjoint cyclic form. A separate tutorial "Permutations" explains how to work with permutations in cyclic form.
Generating Sets
A simple and compact way of specifying a group is by giving a set of elements whose repeated product produces the whole group. These are then called generators of the group and the set of elements is referred to as a generating set. This is a powerful and general method to specify a finite group, though for large groups it might be difficult to extract information from them about the group.
PermutationGroup
head for a permutation group defined by generators
GroupElements
list of elements of a group
GroupMultiplicationTable
table with all multiplications of pairs of elements of a group
CayleyGraph
graph of generator links between elements of a group
Group representations.
Take two permutations and construct the group generated by them:
This is the list of all permutations in the group:
Both generators fix point 2, thus so do all permutations in the group. This generated group is isomorphic to the symmetric group on the set 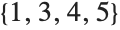, with permutations:
For small groups, it is possible to construct better representations of a group. They are the Cayley multiplication table and Cayley graph, the latter representing mixed information about both the whole group and the generating set being used.
For small groups, all products can be represented using a Cayley multiplication table:
Each row and each column is itself a permutation of the numbers 1–24. The array is symmetric if and only if the group is Abelian. The group 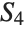is not Abelian:
You can also use a Cayley graph. Multiplication by permutation 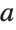is represented in red and by 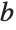in blue:
It is clear in the graph that the first generator (in red) has order 3 and the second one (in blue) has order 2:
Any closed loop in the graph represents a relation giving the identity. For example, the loop 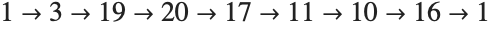corresponds to the following:
In other words, a permutation of order 4 has been found:
Orbits and Stabilizers
Given any generating set of a permutation group acting on a set of points, it is possible to find which other points can be related with a given point. This is called the orbit of that point.
GroupOrbits
compute orbits of points under a group
Orbit computation.
Take two new permutations and form a generating set with them:
This is the orbit of point 3. Orbits are given with points sorted lexicographically:
Each of the points in the orbit uniquely identifies the same orbit:
Points cannot belong to two different orbits and hence orbits partition the set of points on which the group acts.
In this example the maximum point of the support is 30:
Hence, the orbits partition the range of the first 30 points:
Orbits can be selected by supplying more points:
If a larger range is partitioned, all other points are stable:
Orbits can be computed efficiently, and hence it is possible to work with permutations of large support.
Take a group generated by two random permutations of equal large degree:
In most cases the group acts transitively, with a single orbit:
Now take two generators of very different support length:
Then usually there is still one large orbit, but not of maximal length:
Using more general actions it is possible to form other types of orbits, like conjugacy classes.
This is the conjugacy class of a permutation in the symmetric group:
Complementary to the information given by orbits, describing how points move, it is also possible to compute stabilizers, namely the subgroups of elements fixing one or several points.
GroupStabilizer
subgroup of elements fixing one or several points
Computation of stabilizers.
Take this group again:
This is the subgroup of permutations fixing point 3. The cyclic notation shows that none of its generators moves point 3:
Recall the orbit of point 3 under this group has length 18:
By the orbit stabilizer theorem, that must be also the quotient between the group orders:
Strong Generating Set Representation
For larger permutation groups it becomes increasingly infeasible to list or draw all their elements. In such cases it is necessary to resort to alternative methods that can infer information about a group from a generating set of the group without actually computing all its permutations. The key ideas were developed in the late 1960s, and are based on the construction of a new equivalent generating set for the same group, but from which it is easy to form a hierarchy of subgroups that allow fast manipulation of the full group. This special type of generating set is called a strong generating set.
GroupOrder
number of elements of a group
GroupElementQ
test whether a permutation belongs to a given group
Basic functionality with strong generating set representations.
Take this group generated by two permutations with support {1,…,24}:
Orbit computations can be done directly from standard generators. However, in order to compute the group order, the Wolfram Language internally computes strong generators for the group:
That representation is stored, to avoid recomputing it for the same original set of generators:
Now it is possible to do things like testing for membership:
Any product of generators must belong to the group:
Now return to the properties of a strong generating set. Strong generators are defined with respect to a base: this is an ordered subset of points of the domain of action of the group, such that the identity is the only element that fixes them all. That implies that knowing the images of the points in a base under a permutation uniquely identifies that permutation. Groups for which a short base is known can be manipulated highly efficiently. The base defines a very useful hierarchy of stabilizer subgroups, known as the stabilizer chain, which plays a central role in the manipulation of permutation groups, very much like the Gauss-elimination hierarchy of vector spaces in linear algebra. Finally, the condition that characterizes a set of generators as being strong with respect to a base is that it contains generating subsets for all subgroups in the corresponding stabilizer chain.
GroupStabilizerChain
chain of stabilizer subgroups of a permutation group
GroupActionBase
option specifying a base of a group
Stabilizer chain, base, and strong generators.
This is a stabilizer chain of the previous group, with respect to a base {1,2,3} automatically chosen by the Wolfram Language:
These are the orders of the subgroups in the stabilizer chain:
The base and strong generators of the chain can be extracted as follows:
Those are still generators for the original group:
The second group in the chain is the stabilizer of 1, a subgroup of order 253:
The stabilizer subgroup has two permutations less, precisely those moving point 1:
The other permutations in the strong generating set do not move point 1:
You can repeat the stabilization for the first two points in the base:
Finally, the third stabilizer is the trivial group, because it is the stabilizer of the full base:
Check Lagrange's theorem by showing that the size of a subgroup always divides that of the group:
The product of those numbers is the size of the full original group:
The option GroupActionBase allows specifying an alternative base. If it is not a true base, the Wolfram Language will complete it with additional points:
Example: The Rubik Group
One of the most famous permutation groups is that associated with the rotations of a Rubik cube. In the following diagram moving facelets are numbered from 1 to 48. The central facelets do not move, and define six respective basic rotations.

These are the six basic rotations:
This is the number of elements in that group:
Internally the following chain of stabilizers has been constructed. The number of permutations that fix the corresponding list of points is indicated. The last line gives a base of the group, because only one permutation (the identity) fixes the given 18 points:
A set of strong generators is given by the group in the first line of the chain:
Now you can test membership of some moves. For example, swapping two neighbor edge facelets is not allowed:
But the simultaneous switching of two of those is allowed:
This is the superflip move, which switches all those pairs simultaneously:
Other Examples
These are two examples of groups of larger support, but with very short bases.
The largest symplectic group given in the ATLAS of Finite Groups is , represented as permutations on 496 points:
These are the orders of the subgroups in its stabilizer chain:
This is the exceptional twisted group , represented with permutations on 819 points:
It also admits a very short base: