PowerExpand[expr]
expands all powers of products and powers.
PowerExpand[expr,{x1,x2,…}]
expands only with respect to the variables xi.


PowerExpand
PowerExpand[expr]
expands all powers of products and powers.
PowerExpand[expr,{x1,x2,…}]
expands only with respect to the variables xi.
Details and Options

- PowerExpand converts
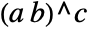 to
to 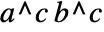 , whatever the form of
, whatever the form of 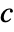 is.
is. - PowerExpand also converts
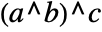 to
to 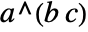 , whatever the form of
, whatever the form of 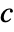 is.
is. - The transformations made by PowerExpand are correct in general only if
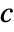 is an integer or
is an integer or 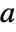 and
and 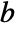 are positive real numbers.
are positive real numbers. - PowerExpand converts Log[a^b] to bLog[a].
- PowerExpand in general disregards all issues of branches of multivalued functions, so may not preserve the numerical values of expressions.
- PowerExpand automatically threads over lists, as well as equations, inequalities and logic functions.
- PowerExpand has the option Assumptions, specifying assumptions to use.
- The default setting for the Assumptions option is Automatic, corresponding to a maximal set of assumptions.
- With Assumptionsassum, the transformations made by PowerExpand are correct whenever the assumptions assum are satisfied.
- With Assumptions:>$Assumptions, you can specify default assumptions for PowerExpand using Assuming.
Examples
open all close allBasic Examples (1)
Expand a square root, implicitly assuming positive real values:
Without PowerExpand, no expansion is done:
The expansion is only correct for positive real variables:
This gives a completely correct result:
This gives a result correct under the specified assumptions:
Scope (11)
Expand a power of a product; the result may not be correct everywhere:
The general formula for expanding a power of a product:
Expand nested powers; the results may not be correct everywhere:
General formulas for expanding a nested power:
Expand the logarithm of a power; the result may not be correct everywhere:
The general formulas for expanding logarithms of powers:
Expand the logarithm of a product; the result may not be correct everywhere:
The general formula for expanding the logarithm of a product:
Expand compositions of inverse trigonometric and trigonometric functions:
This gives the universally correct formula:
Compute an expansion valid under the specified assumptions:
Options (3)
Assumptions (3)
With the default setting Assumptions -> Automatic, the expansions are not always correct:
When the assumptions are specified, the result is correct under the given assumptions:
With Assumptions->True, PowerExpand gives a universally correct expansion formula:
Properties & Relations (5)
PowerExpand performs expansions valid under the given assumptions:
With Assumptions->True, PowerExpand gives general expansion formulas:
Refine and Simplify perform expansions valid under the given assumptions:
Use FunctionExpand to get a different representation of ![]() :
:
Use PiecewiseExpand to represent the result as a piecewise function:
Possible Issues (1)
The result given by PowerExpand with Assumptions->Automatic may be incorrect:
See Also
Expand Power Sqrt Distribute ComplexExpand Simplify FullSimplify FunctionExpand Refine
Function Repository: LogContract
Related Guides
History
Introduced in 1991 (2.0) | Updated in 1996 (3.0) ▪ 2007 (6.0)
Text
Wolfram Research (1991), PowerExpand, Wolfram Language function, https://reference.wolfram.com/language/ref/PowerExpand.html (updated 2007).
CMS
Wolfram Language. 1991. "PowerExpand." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/PowerExpand.html.
APA
Wolfram Language. (1991). PowerExpand. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PowerExpand.html
BibTeX
@misc{reference.wolfram_2025_powerexpand, author="Wolfram Research", title="{PowerExpand}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/PowerExpand.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_powerexpand, organization={Wolfram Research}, title={PowerExpand}, year={2007}, url={https://reference.wolfram.com/language/ref/PowerExpand.html}, note=[Accessed: 04-March-2026]}