DifferentialRoot[lde][x]
gives the holonomic function ![]() , specified by the linear differential equation lde[h,x].
, specified by the linear differential equation lde[h,x].
DifferentialRoot[lde]
represents a pure holonomic function ![]() .
.


DifferentialRoot
DifferentialRoot[lde][x]
gives the holonomic function ![]() , specified by the linear differential equation lde[h,x].
, specified by the linear differential equation lde[h,x].
DifferentialRoot[lde]
represents a pure holonomic function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation; also known as holonomic function and D-finite function.
- The holonomic function
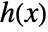 defined by a DifferentialRoot function satisfies a holonomic differential equation
defined by a DifferentialRoot function satisfies a holonomic differential equation 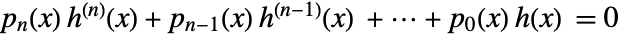 with polynomial coefficients
with polynomial coefficients 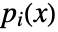 and initial values
and initial values 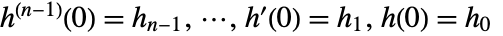 .
. - DifferentialRoot can be used like any other mathematical function.
- FunctionExpand will attempt to convert DifferentialRoot functions in terms of special functions.
- The functions representable by DifferentialRoot include a large number of special functions.
- DifferentialRootReduce can convert most special functions to DifferentialRoot functions.
- Holonomic functions are closed under many operations, including:
-
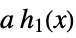 ,
, 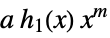
constant multiple, integer power 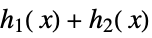 ,
, 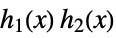
sums and products 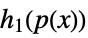 ,
, 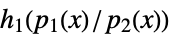 ,
, 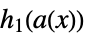
composition with polynomial, rational, and algebraic functions 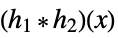
convolution 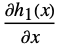 ,
, 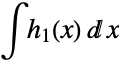
derivatives and integrals - DifferentialRoot is automatically generated by functions such as Integrate, DSolve, and GeneratingFunction.
- Functions such as Integrate, D, SeriesCoefficient, and DSolve work with DifferentialRoot inputs.
- DifferentialRoot can be evaluated to arbitrary numerical precision.
- DifferentialRoot automatically threads over lists.
- DifferentialRoot[lde,pred] represents a solution restricted to avoid cuts in the complex
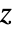 plane defined by pred[z], where pred[z] can contain equations and inequalities.
plane defined by pred[z], where pred[z] can contain equations and inequalities.
Examples
open all close allBasic Examples (2)
Scope (23)
Numerical Evaluation (7)
Evaluate at machine precision:
The precision of the output tracks the precision of the input:
DifferentialRoot takes complex number parameters and arguments:
DifferentialRoot takes inexact input parameters:
Evaluate DifferentialRoot efficiently at high precision:
DifferentialRoot threads elementwise over lists and matrices:
Function Properties (5)
DifferentialRoot objects have all the standard features of a mathematical function:
Simple exact values are generated automatically:
Use FunctionExpand to attempt to convert a DifferentialRoot object to a built-in mathematical function:
DifferentialRoot works on equations with rational coefficients:
Inhomogeneous holonomic equations are automatically transformed to higher-order homogeneous ones:
Differentiation (4)
The derivative of DifferentialRoot is a DifferentialRoot function:
Differentiate a DifferentialRoot object with respect to a parameter:
Compute higher-order derivatives of a DifferentialRoot object:
Differentiate a DifferentialRoot object:
Integration (4)
The integral of a DifferentialRoot object is a DifferentialRoot object:
Compute higher-order integrals of a DifferentialRoot object:
Compute the definite integral of a DifferentialRoot object:
Integrate a DifferentialRoot object:
Series Expansions (3)
Calculate the series expansion of a DifferentialRoot object:
Find the ![]()
![]() coefficient of the Taylor expansion of a DifferentialRoot object:
coefficient of the Taylor expansion of a DifferentialRoot object:
Calculate the first 9 coefficients:
Compare with the Sin function expansion coefficients:
Calculate the series expansion of a DifferentialRoot object with a parameter:
Generalizations & Extensions (1)
Applications (4)
Generate a DifferentialRoot object from a special function:
DifferentialRoot objects have all the standard features of a mathematical function:
Find the coefficients of the series expansion of a DifferentialRoot object:
Calculate the first 5 coefficients of the expansion explicitly:
Compute arbitrary-order derivatives of a DifferentialRoot object:
Integrate the DifferentialRoot object:
Extract the differential equation and initial conditions of the function that is the integral of f:
Plot the function f, its integral and derivative functions:
Use DifferentialRoot to homogenize a differential equation:
Extract the homogenized equation:
Generate a DifferentialRoot object that is a combination of two mathematical functions:
Extract the differential equation and initial conditions that this function obeys:
Properties & Relations (5)
DifferentialRootReduce generates DifferentialRoot objects:
DSolve generates a DifferentialRoot object if the solution is not available in known functions:
GeneratingFunction may generate a DifferentialRoot object:
Integrate returns a DifferentialRoot object for general holonomic functions:
D returns a DifferentialRoot object for general holonomic functions:
Possible Issues (3)
DifferentialRoot takes only linear differential equations with polynomial coefficients:

DifferentialRoot will not evaluate if the initial values are given at a singular point:
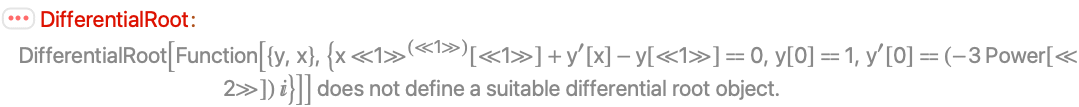
The branch cut structure of a built-in function may differ from the automatically computed branch cut structure:
For some regions of the complex plane, the value of f differs from corresponding built-in function value:
For other regions, DifferentialRoot will give the same result:
Tech Notes
Related Guides
Text
Wolfram Research (2008), DifferentialRoot, Wolfram Language function, https://reference.wolfram.com/language/ref/DifferentialRoot.html (updated 2020).
CMS
Wolfram Language. 2008. "DifferentialRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/DifferentialRoot.html.
APA
Wolfram Language. (2008). DifferentialRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferentialRoot.html
BibTeX
@misc{reference.wolfram_2025_differentialroot, author="Wolfram Research", title="{DifferentialRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DifferentialRoot.html}", note=[Accessed: 23-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_differentialroot, organization={Wolfram Research}, title={DifferentialRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/DifferentialRoot.html}, note=[Accessed: 23-January-2026]}