LogisticDistribution[μ,β]
represents a logistic distribution with mean μ and scale parameter β.
represents a logistic distribution with mean 0 and scale parameter 1.


LogisticDistribution
LogisticDistribution[μ,β]
represents a logistic distribution with mean μ and scale parameter β.
represents a logistic distribution with mean 0 and scale parameter 1.
Details
- LogisticDistribution is also known as sech squared distribution.
- The probability density for value
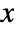 in a logistic distribution is proportional to
in a logistic distribution is proportional to 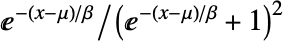 . »
. » - LogisticDistribution allows μ to be any real number and β to be any positive real number.
- LogisticDistribution allows μ and β to be any quantities of the same unit dimensions. »
- LogisticDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- LogisticDistribution[μ,β] represents a continuous statistical distribution defined and supported over the set
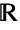 of real numbers and parametrized by a real number μ (called the "mean" of the distribution) and a positive real number β (called a "scale parameter"). Overall, the probability density function (PDF) of a logistic distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of μ and β. In addition, the PDF of the logistic distribution has tails that are "thin" in the sense that its PDF decreases exponentially rather than algebraically for large values of
of real numbers and parametrized by a real number μ (called the "mean" of the distribution) and a positive real number β (called a "scale parameter"). Overall, the probability density function (PDF) of a logistic distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of μ and β. In addition, the PDF of the logistic distribution has tails that are "thin" in the sense that its PDF decreases exponentially rather than algebraically for large values of 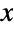 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) So named because its cumulative distribution function (CDF) is a logistic function, the logistic distribution is sometimes referred to as the sech squared distribution, a reference to the fact its PDF can be realized as a constant multiple of the square of the hyperbolic secant (Sech) function. The zero-parameter form LogisticDistribution[] is equivalent to LogisticDistribution[0,1] and is sometimes called the "standard" logistic distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) So named because its cumulative distribution function (CDF) is a logistic function, the logistic distribution is sometimes referred to as the sech squared distribution, a reference to the fact its PDF can be realized as a constant multiple of the square of the hyperbolic secant (Sech) function. The zero-parameter form LogisticDistribution[] is equivalent to LogisticDistribution[0,1] and is sometimes called the "standard" logistic distribution. - The logistic distribution was first investigated by French mathematician Pierre Verhulst in the 1830s and 1840s and was given its name in a 1929 paper by Reed and Berkson. While Verhulst's original interest was in the study of demographics and in the modeling of human populations, one of the main uses of the logistic distribution historically has been in statistics as a tool in so-called logistic regression. Even today, however, the logistic distribution is an often-utilized tool in survival analysis, where it is preferred over qualitatively similar distributions (e.g. the normal distribution (NormalDistribution)) when modeling systems whose failure rates increase over time due to its ability to fit data which is both left- and right-censored. Tools derived from and inspired by the logistic distribution are commonly used to represent tolerance data in various life sciences including zoology and physiology, and the distribution itself is used in mathematical finance to model the risk of various financial assets. The logistic distribution can also model a number of phenomena including the spread of disease, cell growth, and the spread of innovations.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a logistic distribution. Distributed[x,LogisticDistribution[μ,β]] , written more concisely as xLogisticDistribution[μ,β] , can be used to assert that a random variable x is distributed according to a logistic distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for logistic distributions may be given using PDF[LogisticDistribution[μ,β] ,x] and CDF[LogisticDistribution[μ,β] ,x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a logistic distribution, EstimatedDistribution to estimate a logistic parametric distribution from given data, and FindDistributionParameters to fit data to a logistic distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic logistic distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic logistic distribution.
- TransformedDistribution can be used to represent a transformed logistic distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a logistic distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving logistic distributions.
- LogisticDistribution is related to a number of other distributions. LogisticDistribution can be realized as a transformation (TransformedDistribution) of both UniformDistribution and ExponentialDistribution, and can be obtained from various linear combinations of ExponentialDistribution, GumbelDistribution, and ExtremeValueDistribution. The logarithm of a random variate
 that follows LogLogisticDistribution is modeled by LogisticDistribution, and because of the connection of its PDF to hyperbolic secant, LogisticDistribution is also related to SechDistribution. LogisticDistribution is also related to GompertzMakehamDistribution, FrechetDistribution, ParetoDistribution, WeibullDistribution, MaxStableDistribution, and MinStableDistribution.
that follows LogLogisticDistribution is modeled by LogisticDistribution, and because of the connection of its PDF to hyperbolic secant, LogisticDistribution is also related to SechDistribution. LogisticDistribution is also related to GompertzMakehamDistribution, FrechetDistribution, ParetoDistribution, WeibullDistribution, MaxStableDistribution, and MinStableDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from a logistic distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Find the five-number summary of the temperature distribution:
Applications (2)
Logistic distribution can be used to approximate wind speeds:
Find the estimated distribution:
Compare the PDF to the histogram of the wind data:
Find the probability of a day with wind speed greater than 30 km/h:
Simulate wind speeds for a month:
LogisticDistribution provides a very good fit for fractional price changes from the previous closing price of stocks. Find the estimated distribution for the daily fractional price changes of the Standard & Poor's 500 index from January 1, 2000, to January 1, 2009:
Compare a histogram of the data with the PDF of the estimated distribution:
Find the probability of the fractional price change being greater than 0.5%:
Find the mean fractional price change:
Simulate fractional price changes for 30 days:
Logistic distribution provides better fit than the traditionally used NormalDistribution:
Properties & Relations (11)
Logistic distribution is closed under translation and scaling by a positive factor:
The probability density function can be expressed in terms of the square of Sech:
Logistic distribution mimics SechDistribution:
Compare a histogram to the PDF of the estimated distribution:
Comparing the fit with the original distribution:
Relationships to other distributions:
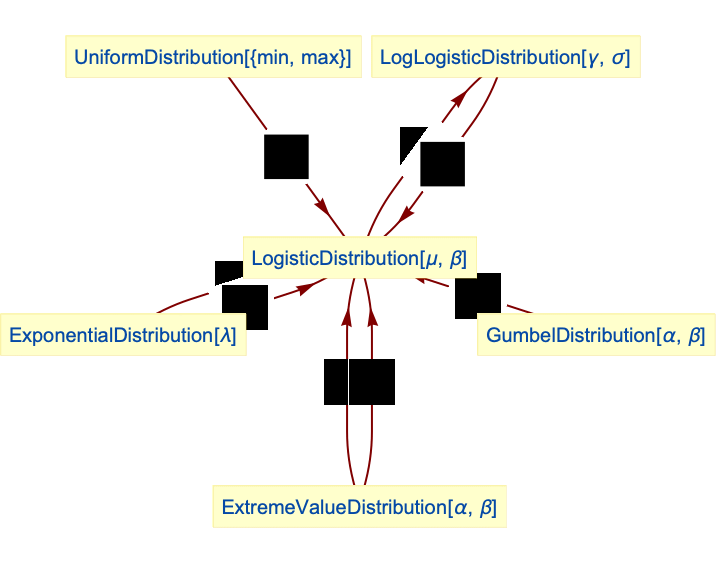
LogisticDistribution is related to LogLogisticDistribution:
Logistic distribution is a transformation of UniformDistribution:
Logistic distribution is a transformation from ExponentialDistribution:
Logistic distribution is a transformation of ExponentialDistribution:
The difference of two variates from GumbelDistribution follows the same distribution as the difference of two variates from ExtremeValueDistribution, which is logistic distribution:
Sum of ExtremeValueDistribution and GumbelDistribution follows logistic distribution:
Logistic distribution is a ParameterMixtureDistribution of ExtremeValueDistribution:
Possible Issues (2)
LogisticDistribution is not defined when μ is not a real number:
LogisticDistribution is not defined when β is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Related Guides
Text
Wolfram Research (2007), LogisticDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LogisticDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "LogisticDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LogisticDistribution.html.
APA
Wolfram Language. (2007). LogisticDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogisticDistribution.html
BibTeX
@misc{reference.wolfram_2025_logisticdistribution, author="Wolfram Research", title="{LogisticDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/LogisticDistribution.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_logisticdistribution, organization={Wolfram Research}, title={LogisticDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/LogisticDistribution.html}, note=[Accessed: 25-January-2026]}