LogLogisticDistribution
represents a log-logistic distribution with shape parameter γ and scale parameter σ.
Details
- LogLogisticDistribution is also known as Fisk distribution.
- The probability density for value
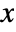in a log-logistic distribution is proportional to 
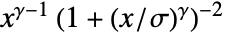for 
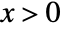. - LogLogisticDistribution allows γ and σ to be any positive real numbers.
- LogLogisticDistribution allows σ to be a quantity of any unit dimension, and γ to be a dimensionless quantity. »
- LogLogisticDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- LogLogisticDistribution[γ,σ] represents a continuous statistical distribution supported over the interval
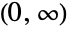and parametrized by positive real numbers γ (called a "shape parameter") and σ (called a "scale parameter"), which together determine the overall behavior of its probability density function (PDF). Depending on the values of γ and σ, the PDF of a log-logistic distribution may be either unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with a potential singularity approaching the lower boundary of its domain. In addition, the PDF of the log-logistic distribution has tails that are "fat" in the sense that its PDF decreases algebraically rather than exponentially for large values of 
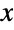. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) LogLogisticDistribution is sometimes referred to as the Fisk distribution, particularly in applications to economics. - LogLogisticDistribution is the distribution followed by the logarithm of a logistic-distributed random variable. In other words, if
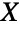is a random variable and 
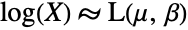(where 
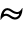denotes "is distributed as"), then 
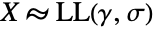. Qualitatively, the log-logistic distribution is similar to the log-normal distribution (LogNormalDistribution) and as such, both are commonly utilized tools for approximating lifetime data across various disciplines. In addition, the log-logistic distribution has been employed to model numerous phenomena including precipitation, wealth and income distribution, and data transmission and processing times. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a log-logistic distribution. Distributed[x,LogLogisticDistribution[γ,σ]], written more concisely as xLogLogisticDistribution[γ,σ], can be used to assert that a random variable x is distributed according to a log-logistic distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for log-logistic distributions may be given using PDF[LogLogisticDistribution[γ,σ],x] and CDF[LogLogisticDistribution[γ,σ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a log-logistic distribution, EstimatedDistribution to estimate a log-logistic parametric distribution from given data, and FindDistributionParameters to fit data to a log-logistic distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic log-logistic distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic log-logistic distribution.
- TransformedDistribution can be used to represent a transformed log-logistic distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a log-logistic distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving log-logistic distributions.
- LogLogisticDistribution is related to a number of other distributions. LogLogisticDistribution is connected to LogisticDistribution and is qualitatively similar to LogNormalDistribution as discussed above. LogLogisticDistribution is a special case of several distributions including DagumDistribution, SinghMaddalaDistribution, and BetaPrimeDistribution in the sense that the PDF of LogLogisticDistribution[γ,σ] is precisely the same as that of DagumDistribution[1,γ,σ], SinghMaddalaDistribution[1,γ,σ], and BetaPrimeDistribution[1,1,γ,σ]. Its logarithmic behavior is qualitatively similar to that of LogGammaDistribution, LogMultinormalDistribution, and LogNormalDistribution. LogLogisticDistribution is also related to DavisDistribution, NormalDistribution, ExponentialDistribution, WeibullDistribution, GompertzMakehamDistribution, and GammaDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a log-logistic distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the shape parameter γ:
For large values of γ, log-logistic distribution becomes symmetric:
Kurtosis depends only on the shape parameter γ:
Kurtosis has horizontal asymptote as γ gets large:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
LogLogisticDistribution can be used to model incomes:
Adjust part-time to full-time and select nonzero values, attach currency unit:
Fit log-logistic distribution to the data:
Compare the histogram of the data to the PDF of the estimated distribution:
Find the average income at a large state university:
Find the probability that a salary is at most $15,000:
Find the probability that a salary is at least $150,000:
Simulate the incomes for 100 randomly selected employees of such a university:
BetaPrimeDistribution can be used to model state per capita incomes:
Fit log-logistic distribution to the data:
Compare the histogram of the data to the PDF of the estimated distribution:
Find the average income per capita:
Find states with income close to the average:
Find the median income per capita:
Properties & Relations (6)
Log-logistic distribution is closed under scaling by a positive factor:
Relationships to other distributions:
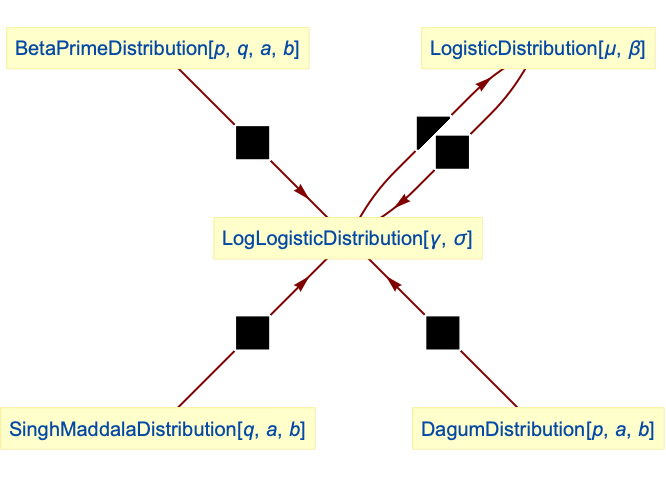
LogLogisticDistribution is a special case of DagumDistribution:
LogLogisticDistribution is a special case of SinghMaddalaDistribution:
LogLogisticDistribution is a special case of BetaPrimeDistribution:
LogLogisticDistribution is related to LogisticDistribution:
Text
Wolfram Research (2010), LogLogisticDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LogLogisticDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "LogLogisticDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LogLogisticDistribution.html.
APA
Wolfram Language. (2010). LogLogisticDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogLogisticDistribution.html