ParameterMixtureDistribution

ParameterMixtureDistribution[dist[θ],θwdist]

represents a parameter mixture distribution where the parameter θ is distributed according to the weight distribution wdist.

ParameterMixtureDistribution[dist[θ1,θ2,…],{θ1wdist1,θ2wdist2,…}]

represents a parameter mixture distribution where the parameter θ1 has weight distribution wdist1, θ2 has weight distribution wdist2, etc.

Details and Options

  • The probability density for value 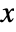is given by Expectation[PDF[dist[θ],x],θwdist].
  • The domain of the weight distribution wdist needs to be a subset or equal to the parameter domain expected for dist[θ].
  • Parameters θi can be discrete or continuous.
  • Assumptions on parameters can be specified using the option Assumptionsassum.
  • ParameterMixtureDistribution can be used with such functions as Mean, CDF, and RandomVariate, etc.

Examples

open allclose all

Basic Examples  (3)

Specify a parameter mixture distribution:

Parameter mixture distributions work like any other distributions:

Find a parameter mixture of a multivariate distribution:

Scope  (36)

Basic Uses  (7)

Find the parameter mixture of ExponentialDistribution with uniformly distributed weight:

Probability density function:

The weight domain must satisfy the parameter assumptions of the main distribution:

Pick a weight distribution supported on the positive reals:

The resulting parameter mixture CDF:

Use a discrete weight for a discrete parameter:

Compare the probability density functions:

Compare probabilities of obtaining a value less than 4 from each distribution:

Vary only one parameter:

Cumulative distribution function:

Mean and variance:

Use a multivariate distribution as a weight to vary more than one parameter:

Use more than one weight distribution to vary multiple parameters:

Visualize the probability density function:

Estimate parameters in a parameter mixture distribution:

Create a random sample for a choice of weight distribution parameters:

Find the distribution parameters:

Compare the histogram of the sample with the PDF of the estimated distribution:

Weight Distributions  (5)

Define a parameter mixture with a continuous univariate weight distribution:

Define a parameter mixture with a discrete univariate weight distribution:

Find the probability density function:

Moment has closed form for a symbolic order:

Define a parameter mixture with a discrete univariate weight distribution:

Probability density function:

Define a parameter mixture with a multivariate weight distribution:

Probability density function:

Verify that the integral of the PDF is 1:

Use more than one weight distribution:

Mean:

Variance:

Parametric Distributions  (8)

Define a parameter mixture of a continuous univariate distribution:

Cumulative distribution function:

Find a mixture of a continuous univariate distribution:

Probability density function:

Define a parameter mixture of a discrete univariate distribution:

Generate a random sample:

Find the mean and variance:

Find a parameter mixture of a discrete univariate distribution:

Probability density function:

Mean and variance:

For a fixed value of , Moment has closed form for symbolic order:

Define a parameter mixture of a bivariate continuous distribution:

Use a random sample and a smooth histogram to visualize the density function:

Define a parameter mixture of a bivariate distribution:

Probability density function:

Mean:

Covariance matrix:

Find a parameter mixture distribution of a multivariate discrete distribution:

Generate a random sample:

Histograms for each component:

LaplaceDistribution can be represented as a parametric mixture:

Nonparametric Distributions  (3)

Use an EmpiricalDistribution as a weight:

Probability density function:

Use a HistogramDistribution as a weight:

Probability density function:

Define a parameter mixture with a SmoothKernelDistribution as a weight:

Plot the probability density function:

Plot the cumulative distribution function:

Derived Distributions  (11)

Use a ProductDistribution as a weight distribution in a parameter mixture:

Use the histogram of a random sample from to visualize the PDF:

Find a parameter mixture distribution of a TransformedDistribution:

Visualize the density function using a random sample:

Find a parameter mixture using a TransformedDistribution as a weight distribution:

Probability density function:

Use a MixtureDistribution as a weight distribution in a parameter mixture:

Probability density function:

Mean and variance:

Vary weights in a MixtureDistribution according to a probability distribution:

Probability density function:

Compare to the MixtureDistribution with fixed weights at the average values:

Both density functions are equal:

Define a parameter mixture of a TruncatedDistribution:

Mean and variance:

Define a parameter distribution of a TruncatedDistribution:

Visualize the probability density function using random sample:

Use a TruncatedDistribution as a weight distribution in a parameter mixture:

Probability density function:

Mean:

Find a parameter mixture distribution of an OrderDistribution:

Probability density function:

Use an OrderDistribution as a weight distribution:

Probability density function:

Parameter mixture of QuantityDistribution evaluates to QuantityDistribution:

Automatic Simplifications  (2)

Discrete Distributions  (1)

Parameter mixtures with BetaDistribution as a weight:

Parameter mixtures involving PoissonDistribution:

Continuous Distributions  (1)

Parameter mixtures of RayleighDistribution:

Parameter mixtures of NormalDistribution:

Options  (1)

Assumptions  (1)

WaringYuleDistribution is a parameter mixture of geometric distribution and UniformDistribution:

Compare with the built-in answer:

Applications  (7)

SuzukiDistribution is defined as a parameter mixture of RayleighDistribution and LogNormalDistribution:

KDistribution can be represented as a parameter mixture of RayleighDistribution and GammaDistribution:

The time in minutes it takes a bank teller to serve a customer follows ExponentialDistribution, with average time having LindleyDistribution with mean 3. Find the service time distribution:

Probability density function:

The average service time:

Simulate the service time for the next 30 customers:

In an optical communication system, transmitted light generates current at the receiver. The number of electrons follows the parametric mixture of a Poisson distribution and another distribution, depending on the type of light. If the source uses coherent laser light of intensity , then the electron-count distribution is Poisson:

Which is PoissonDistribution:

If the source uses thermal illumination, then the Poisson parameter follows ExponentialDistribution with parameter , and the electron count distribution can be determined:

These two distributions are distinguishable and allow you to determine the type of source:

The Voigt spectral line profile results from combining a Doppler (Cauchy) profile and a Lorentzian (normal) profile:

Compute the density function:

Plot the density function:

Compute the profile half-width:

Define modified normal distribution:

Plot modified normal distribution densities for several values of and compare them with standard normal density:

Define multivariate Pólya distribution:

Probability density function:

Properties & Relations  (4)

The PDF of a parameter mixture can be computed using Expectation:

Parameter mixture with a discrete weight, assuming a finite number of values can be represented as a MixtureDistribution:

Compare PDFs:

Parameter mixture with a discrete weight, assuming a countable number of values can be approximated by a MixtureDistribution:

Compare approximations for different quantiles as cut-offs:

Approximating a parameter mixture with a continuous weight by a MixtureDistribution:

Compare PDFs:

Wolfram Research (2010), ParameterMixtureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html (updated 2016).

Text

Wolfram Research (2010), ParameterMixtureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "ParameterMixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html.

APA

Wolfram Language. (2010). ParameterMixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html

BibTeX

@misc{reference.wolfram_2024_parametermixturedistribution, author="Wolfram Research", title="{ParameterMixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parametermixturedistribution, organization={Wolfram Research}, title={ParameterMixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}, note=[Accessed: 21-November-2024 ]}