SmoothKernelDistribution[{x1,x2,…}]
represents a smooth kernel distribution based on the data values xi.
SmoothKernelDistribution[{{x1,y1,…},{x2,y2,…},…}]
represents a multivariate smooth kernel distribution based on the data values {xi,yi,…}.
SmoothKernelDistribution[…,bw]
represents a smooth kernel distribution with bandwidth bw.
SmoothKernelDistribution[…,bw,ker]
represents a smooth kernel distribution with bandwidth bw and smoothing kernel ker.


SmoothKernelDistribution
SmoothKernelDistribution[{x1,x2,…}]
represents a smooth kernel distribution based on the data values xi.
SmoothKernelDistribution[{{x1,y1,…},{x2,y2,…},…}]
represents a multivariate smooth kernel distribution based on the data values {xi,yi,…}.
SmoothKernelDistribution[…,bw]
represents a smooth kernel distribution with bandwidth bw.
SmoothKernelDistribution[…,bw,ker]
represents a smooth kernel distribution with bandwidth bw and smoothing kernel ker.
Details and Options




- SmoothKernelDistribution returns a DataDistribution object that can be used like any other probability distribution.
- The probability density function for SmoothKernelDistribution for a value
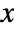 is given by a linearly interpolated version of
is given by a linearly interpolated version of 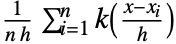 for a smoothing kernel
for a smoothing kernel 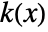 and bandwidth parameter
and bandwidth parameter 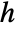 .
. - The following bandwidth specifications bw can be given:
-
h bandwidth to use {"Standardized",h} bandwidth in units of standard deviations {"Adaptive",h,s} adaptive with initial bandwidth h and sensitivity s Automatic automatically computed bandwidth "name" use a named bandwidth selection method {bwx,bwy,…} separate bandwidth specifications for x, y, etc. - For multivariate densities, h can be a positive definite symmetric matrix.
- For adaptive bandwidths, the sensitivity s must be a real number between 0 and 1 or Automatic. If Automatic is used, s is set to
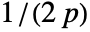 , where
, where 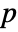 is the dimensionality of the data.
is the dimensionality of the data. - Possible named bandwidth selection methods include:
-
"LeastSquaresCrossValidation" use the method of least-squares cross-validation "Oversmooth" 1.08 times wider than the standard Gaussian "Scott" use Scott's rule to determine bandwidth "SheatherJones" use the Sheather–Jones plugin estimator "Silverman" use Silverman's rule to determine bandwidth "StandardDeviation" use the standard deviation as bandwidth "StandardGaussian" optimal bandwidth for standard normal data - By default, the "Silverman" method is used.
- For automatic bandwidth computation, constant arrays are assumed to have unit variance.
- The following kernel specifications ker can be given:
-
"Biweight" 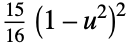
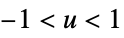
"Cosine" 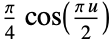
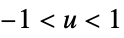
"Epanechnikov" 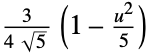
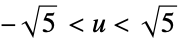
"Gaussian" 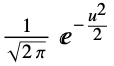
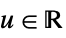
"Rectangular" 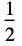
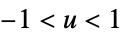
"SemiCircle" 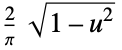
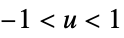
"Triangular" 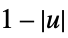
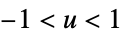
"Triweight" 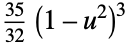
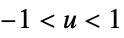
func 
- In order for SmoothKernelDistribution to generate a true density estimate, the function fn should be a valid probability density function.
- By default, the "Gaussian" kernel is used.
- The kernel function ker can be specified to account for known bounding on the underlying density using {"Bounded",c,ker}, where c can be any real number, a list {c1,c2} such that c1<c2, or a list {{c11,c12},{c21,c22},…}, with length equal to the dimension of data.
- For multivariate densities, the kernel function ker can be specified as product and radial types using {"Product",ker} and {"Radial",ker}, respectively. Product-type kernels are used if no type is specified.
- The precision used for density estimation is the minimum precision given in the bw and data.
- The following options can be given:
-
InterpolationPoints Automatic initial number of interpolation points to use MaxMixtureKernels Automatic max number of kernels to use MaxRecursion Automatic number of recursive subdivisions to allow PerformanceGoal Automatic optimize for speed or quality MaxExtraBandwidths Automatic max bandwidths beyond data to use - SmoothKernelDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Examples
open all close allBasic Examples (2)
Create an interpolated version of a kernel density estimate for some univariate data:
Use the resulting distribution to perform analysis, including visualizing distribution functions:
Compute moments and quantiles:
Create an interpolated version of a kernel density estimate of some bivariate data:
Scope (37)
Basic Uses (7)
Create an interpolated smooth density estimate for some data:
Compute probabilities from the distribution:
Create an interpolated version of a kernel density estimate for data with quantities:
Increase the bandwidth for smoother estimates:
Allow the bandwidth to vary adaptively with local density:
Interpolate kernel density estimates in higher dimensions:
Plot the univariate marginal PDFs:
Plot the bivariate marginal PDFs:
Select from built-in kernel functions or build a custom one:
Specify radial- or product-type kernels for multivariate estimates:
Distribution Properties (8)
Estimate distribution functions:
Compute moments of the distribution:
Compare with SmoothKernelDistribution:
Compute probabilities and expectations:
Estimate bivariate distribution functions:
Bandwidth Selection (12)
Automatically select the bandwidth to use:
More data yields better approximations to the underlying distribution:
Explicitly specify the bandwidth to use:
Larger bandwidths yield smoother estimates:
Specify bandwidths in units of standard deviation:
Use bandwidths of ![]() and
and ![]() the standard deviation:
the standard deviation:
Allow the bandwidth to vary adaptively with local density:
Vary the local sensitivity from 0 (none) to 1 (full):
Vary the initial bandwidth for an adaptive estimate:
Specify an initial bandwidth of 1.0 and 0.1, respectively:
Use any of several automatic bandwidth selection methods:
Silverman's method is used by default:
By default, Silverman's method is used to independently select bandwidths in each dimension:
Any automated method can be used to independently select diagonal bandwidth elements:
Methods used to estimate the bandwidth diagonal need not be the same:
Use adaptive, oversmoothed, and constant bandwidths in the respective dimensions:
Plot the univariate marginal PDFs:
Give a scalar value to use the same bandwidth in all dimensions:
To use nonzero off-diagonal elements, give a fully specified bandwidth matrix:
Kernel Functions (6)
Specify any one of several kernel functions:
Define the kernel function as a pure function:
By default, the Gaussian kernel is used:
This is equivalent to using the PDF of a NormalDistribution[0,1]:
Shapes of some univariate kernel functions:
Specify any one of several kernel functions for multivariate data:
Choose between product- and radial-type kernel functions for multivariate data:
Estimation with Fixed Domain (4)
Use bounding to stay within the domain:
Define the smooth kernel distribution with a Gaussian kernel:
The support for PDF extends beyond the data support:
Compare to the original BetaDistribution:
Compare smooth kernel distributions with a bounded Epanechnikov kernel:
The bounded smooth kernel density estimate is more accurate at the boundaries:
Use a bounded cosine kernel for two-dimensional data:
Compare the estimated density to the population distribution density:
Truncating the ordinary smooth kernel distribution yields a different result:
Options (25)
InterpolationPoints (6)
By default, nonuniform interpolation is used to create a smooth estimate:
Specify the initial number of sample points to use:
A larger number of points yields a smoother estimate:
Specify the number of interpolating points to use for bivariate data:
Use 5 and 50 interpolation points in each dimension:
Use different numbers of interpolation points in each dimension:
Specify 3 and 30 points or 30 and 3:
A smooth result does not imply a high-quality estimate:
Using 1000 interpolation points creates a very smooth estimate in this case:
MaxExtraBandwidths (6)
By default, the estimate extends at most 12 bandwidths beyond the data:
Set the maximum number of bandwidths to use:
Use 0 and 12 bandwidths, respectively:
Set a different number for each endpoint:
Specify the number of extra bandwidths to use for multivariate data:
Use 0 and 12 bandwidths, respectively:
Specify the number of extra bandwidths to use in each dimension:
Use 0 and 12 bandwidths or 12 and 0 bandwidths, respectively:
MaxMixtureKernels (6)
By default, the number of kernels is generally optimal:
Specify the maximum number of kernels to use in the estimate:
A larger number of kernels gives a better estimate of the underlying distribution:
Place a kernel at each data point:
Vary the bandwidth used for the same number of kernels:
Specify the maximum number of kernels to use in each dimension for bivariate data:
Place at most 10 and 100 kernels, respectively:
MaxRecursion (4)
A smooth estimate will usually be returned by default:
Specify the maximum number of recursive subdivisions to use:
Give the maximum number of recursive subdivisions for bivariate data:
Use at most 2 and 6 subdivisions, respectively:
Set the maximum number of recursive subdivisions in each dimension:
PerformanceGoal (3)
By default, estimates are optimized for a balance between speed and quality:
Set PerformanceGoal for speed or quality or use Automatic to balance the two:
More time is spent with PerformanceGoal set to "Quality":
Use with ControlActive to vary PerformanceGoal dynamically:
Applications (14)
Compare an estimated density to a theoretical model:
Use adaptive bandwidths for highly oscillatory densities:
The moments of the model and the estimate are similar:
Use TruncatedDistribution to restrict the domain after smoothing:
The estimate is restricted to positive values:
Verify that the distribution is bound by the truncation region:
Use with Cases to restrict the data domain before smoothing:
The estimate goes beyond the data on the left, but the data is restricted to positive values:
The probability that the data falls below zero is not zero:
Use MaxExtraBandwidths to restrict the domain without dropping data:
The estimate stops at the minimum data value, which is restricted to positive values:
Estimate the distribution of the lengths of human chromosomes:
The expected chromosome length, given that the length is greater than the mean:
Smooth the discrete distribution of the differences of successive primes:
Investigate the distribution of differenced daily returns on the S&P 500 during the 1990s:
Compare the smoothed distribution to a fitted model:
Compare the distribution of salaries from two university departments:
Select salaries for two departments and attach currency units:
Estimate the joint distribution of Old Faithful eruption durations and waiting times:
Probability an eruption lasts more than two minutes and the waiting time is less than one hour:
Generate random numbers from the histogram for smoothing:
Smooth an estimate returned from SurvivalDistribution:
Compute the probability of survival beyond 25, given that the survival time is greater than 10:
Create a confidence band for the PDF of snowfall accumulations in Buffalo, New York:
Smooth over each bootstrapped sample and obtain the confidence estimates:
Visualize the estimate of the PDF with the 95% confidence band:
Confirm that the Mahalanobis distance has an asymptotic ChiSquareDistribution[p], given p-dimensional multivariate normal data:
The probability that the Mahalanobis distance will exceed 10, given four-dimensional normal data:
Estimate a heavy-tailed density using parametric tail models:
The body is estimated well, but the tails are undersmoothed due to lack of data:
Create a mixture of the kernel density estimate and estimated tail models:
Properties & Relations (8)
The resulting density estimate integrates to unity:
By default, machine estimates are used:
Use high-precision data to get high-precision estimates:
The CDF and SurvivalFunction are piecewise quadratic:
The HazardFunction is piecewise rational with linear over quadratic:
SmoothKernelDistribution is a consistent estimator of the underlying distribution:
As the bandwidth approaches infinity, the estimate approaches the shape of the kernel:
SmoothKernelDistribution is a linear interpolation of KernelMixtureDistribution:
SmoothKernelDistribution works on the values only when the input is a TimeSeries or an EventSeries:
SmoothKernelDistribution works with all the values together when the input is a TemporalData:
Possible Issues (4)
The kernel function needs to be a PDF:
The resulting density estimate is not a PDF:
Automatic adaptive bandwidths may be too small with large samples:
Try increasing the initial bandwidth, MaxMixtureKernels, or decreasing the sensitivity:
SmoothKernelDistribution does not know the domain of the underlying distribution:
The estimated PDF is continuous, although the underlying distribution is discrete:
The estimated PDF is not bound on ![]() :
:
With heavily adaptive bandwidths, these issues may be less obvious:
The tails of some distributions are too heavy to interpolate effectively:
KernelMixtureDistribution uses symbolic methods that do not rely on interpolation:
Text
Wolfram Research (2010), SmoothKernelDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "SmoothKernelDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html.
APA
Wolfram Language. (2010). SmoothKernelDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html
BibTeX
@misc{reference.wolfram_2025_smoothkerneldistribution, author="Wolfram Research", title="{SmoothKernelDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_smoothkerneldistribution, organization={Wolfram Research}, title={SmoothKernelDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}, note=[Accessed: 11-March-2026]}