represents a Poisson distribution with mean μ.


PoissonDistribution
represents a Poisson distribution with mean μ.
Details
- The probability for integer value
 in a Poisson distribution is
in a Poisson distribution is 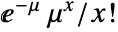 for
for 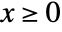 and is zero for
and is zero for 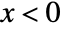 . »
. » - PoissonDistribution allows μ to be any positive real number.
- PoissonDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- PoissonDistribution[μ] represents a discrete statistical distribution defined for integer values
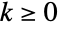 and determined by the positive real parameter μ (the mean of the distribution). The Poisson distribution has a probability density function (PDF) that is discrete and unimodal. It is sometimes referred to as the "classical Poisson distribution" to differentiate it from the more general Poisson–Consul distribution (PoissonConsulDistribution), which is itself sometimes referred to as the "general" Poisson distribution.
and determined by the positive real parameter μ (the mean of the distribution). The Poisson distribution has a probability density function (PDF) that is discrete and unimodal. It is sometimes referred to as the "classical Poisson distribution" to differentiate it from the more general Poisson–Consul distribution (PoissonConsulDistribution), which is itself sometimes referred to as the "general" Poisson distribution. - The derivation of the Poisson distribution dates to the work of French mathematician Abraham de Moivre from 1711. It is, however, named for French mathematician Siméon Poisson because of Poisson's utilization of the distribution to model wrongful convictions in the late 1830s. Classically, the Poisson distribution yields the likelihood of a given number of events occurring in a fixed interval if the events occur independently of the time since the last event and at a known average rate. Because of the techniques used to derive it, the distribution has been extremely useful in modeling situations consisting of a large number of independent trials with a consistent but very small probability of occurrence (e.g. the number of deaths per year of cavalry soldiers stemming from kicks by horse). The Poisson distribution has also been used to model a number of modern phenomena including internet traffic, phone call arrivals, and scoring in sporting events, and is a valuable modeling tool in areas such as finance, biology, physics, and telecommunications.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Poisson distribution. Distributed[x,PoissonDistribution[μ]], written more concisely as xPoissonDistribution[μ], can be used to assert that a random variable x is distributed according to a Poisson distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[PoissonDistribution[μ],x] and CDF[PoissonDistribution[μ],x], though one should note that there is no closed-form expression for its CDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Poisson distribution, EstimatedDistribution to estimate a Poisson parametric distribution from given data, and FindDistributionParameters to fit data to a Poisson distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Poisson distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Poisson distribution.
- TransformedDistribution can be used to represent a transformed Poisson distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Poisson distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Poisson distributions.
- PoissonDistribution is related to a number of other statistical distributions. It is generalized by PoissonConsulDistribution in the sense that the PDF of PoissonDistribution[μ] is precisely that of PoissonConsulDistribution[μ,0]. Moreover, PoissonDistribution is a limiting case for both BinomialDistribution and PolyaAeppliDistribution in the sense that the PDF of BinomialDistribution[n,μ/n] as n→∞ is precisely the same as the PDF of PoissonDistribution[μ], while the PDF for PolyaAeppliDistribution[θ,p] tends to that of PoissonDistribution[θ] as p→0. PoissonDistribution is also related to NegativeBinomialDistribution, GammaDistribution, GeometricDistribution, ExponentialDistribution, BorelTannerDistribution, BinomialDistribution, NegativeMultinomialDistribution, and MultinomialDistribution.
Examples
open all close allBasic Examples (3)
Scope (7)
Generate a sample of pseudorandom numbers from a Poisson distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
A Poisson distribution becomes more symmetric for large values of μ:
Kurtosis of normal distribution is the limiting value for kurtosis of a Poisson distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Applications (14)
CDF of PoissonDistribution is an example of a right-continuous function:
The average number of accidents in a city is 100 per day. Simulate the daily accidents:
Find the probability that there are 90 or more accidents on a single day:
Find the standard deviation of the number of accidents per day:
The expected number of raindrops falling into a bucket in a 5-second interval is 20. Simulate the raindrop count for each 5-second interval:
Find the probability that exactly 20 raindrops fall into the bucket in 5 seconds:
A radioactive material on average emits 3.2 ![]() -particles per second; show the distribution:
-particles per second; show the distribution:
Compute the probability that more than 4 ![]() -particles are emitted over the next second:
-particles are emitted over the next second:
Simulate a typical particle count per second over 10 minutes:
Suppose flaws in plywood occur on average of one flaw per 50 square feet. Simulate the process of finding flaws on a per-square-foot basis:
Find the probability that a 4-foot-by-8-foot sheet will have no flaws:
For a mirror with area 7.54 cm![]() , the probability of no flaws is 0.9100. Using the same polishing process, another mirror with an area of 19.50 cm
, the probability of no flaws is 0.9100. Using the same polishing process, another mirror with an area of 19.50 cm![]() is fabricated. Assuming a Poisson error process, find the probability of no flaws on the larger mirror. Using the conditions for the smaller mirror and with error distribution PoissonDistribution [λ area]:
is fabricated. Assuming a Poisson error process, find the probability of no flaws on the larger mirror. Using the conditions for the smaller mirror and with error distribution PoissonDistribution [λ area]:
The resulting mirror polishing defect distribution is then:
The probability of no errors in the larger mirror:
Typographical errors in a book are occurring randomly according to a Poisson process. On 384 pages, 158 errors are counted. Find the distribution of errors per page where the distribution is of the form PoissonDistribution[λ p], where p is the number of pages:
Find the probability of exactly 0 errors per page:
Find the probability of fewer than 2 errors per page:
Find the probability of 1 or more errors per page:
In modeling an adverse reaction to a medicine, it is determined that on average 2 people per 100000 have the adverse reaction. Assuming a Poisson distribution, find the adverse reaction distribution:
Find the probability that there will be at least 5 adverse reactions when the medicine is administered to 350000 people:
The number of queries ![]() arriving in
arriving in ![]() seconds to a call center is Poisson distributed with parameter
seconds to a call center is Poisson distributed with parameter ![]() , where
, where ![]() is the average arrival rate in queries per second. Assuming that the average arrival rate is 4 queries per minute, find the probability of getting more than 4 queries in 10 seconds:
is the average arrival rate in queries per second. Assuming that the average arrival rate is 4 queries per minute, find the probability of getting more than 4 queries in 10 seconds:
Find the probability that there are fewer than 5 queries in 2 minutes:
The number of packet arrivals ![]() in
in ![]() seconds at a multiplexer is Poisson distributed with parameter
seconds at a multiplexer is Poisson distributed with parameter ![]() , where
, where ![]() is the average arrival rate in packets per second. Find the probability that there are no packet arrivals in
is the average arrival rate in packets per second. Find the probability that there are no packet arrivals in ![]() seconds:
seconds:
Find the probability that ![]() or fewer packets arrive in
or fewer packets arrive in ![]() seconds:
seconds:
A data center has 10000 disk drives. Suppose that a disk fails in a given day with probability ![]() . Find the probability that there are no failures in a given day:
. Find the probability that there are no failures in a given day:
That distribution is closely approximated with a Poisson distribution with parameter ![]() :
:
Find the probability that there are fewer than 10 failures in 2 days:
Find the number of spare disk drives that should be available so that all failures in a day can be replaced with probability 99.9%:
Plot the cumulative probability that the number of failures is less than ![]() :
:
Find the minimum number ![]() for which the probability is greater than 99.9%:
for which the probability is greater than 99.9%:
An LCD display has 1920×1080 pixels. A display is accepted if it has 15 or fewer faulty pixels. The probability that a pixel is faulty from production is ![]() . Find the proportion of displays that are accepted:
. Find the proportion of displays that are accepted:
Find the pixel failure rate required to produce 4000×2000 pixel displays and still have an acceptance rate of at least 90%:
Plot the acceptance rate as a function of the pixel failure rate:
Find the maximal acceptable pixel failure rate:
A switchboard receives on average 100 calls per minute. Find what the switchboard capacity should be so that it gets saturated less than once in every 60 minutes:
Find the minimum capacity that satisfies the constraint:
In an optical communication system, transmitted light generates current at the receiver. The number of electrons follows the parametric mixture of a Poisson distribution and another distribution, depending on the type of light. If the source uses coherent laser light of intensity ![]() , then the electron count distribution is Poisson:
, then the electron count distribution is Poisson:
Which is PoissonDistribution:
If the source uses thermal illumination, then the Poisson parameter follows ExponentialDistribution with parameter ![]() and the electron count distribution is:
and the electron count distribution is:
These two distributions are distinguishable and allow you to determine the type of source:
Properties & Relations (11)
The sum of Poisson variables is Poisson distributed:
Relationships to other distributions:
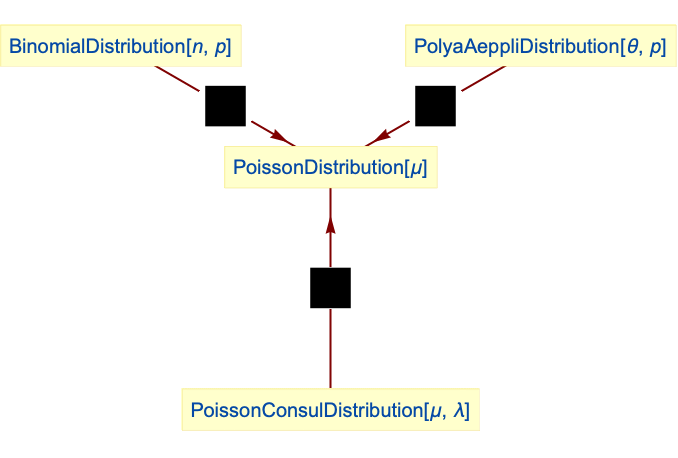
PoissonDistribution is a limiting case for BinomialDistribution with ![]() :
:
PoissonConsulDistribution simplifies to Poisson distribution:
Poisson distribution is a limiting case for PolyaAeppliDistribution:
NegativeBinomialDistribution is a mixture of PoissonDistribution and GammaDistribution:
GeometricDistribution is a mixture of PoissonDistribution and GammaDistribution:
The parametric mixture of Poisson distribution and ExponentialDistribution follows GeometricDistribution:
PoissonConsulDistribution is a parameter mixture of BorelTannerDistribution and PoissonDistribution:
The limit of NegativeBinomialDistribution when the mean is fixed is Poisson distribution:
For large μ, the PoissonDistribution can be approximated by NormalDistribution:
Possible Issues (2)
PoissonDistribution is not defined when μ is non-positive:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
History
Text
Wolfram Research (2007), PoissonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonDistribution.html.
CMS
Wolfram Language. 2007. "PoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonDistribution.html.
APA
Wolfram Language. (2007). PoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonDistribution.html
BibTeX
@misc{reference.wolfram_2025_poissondistribution, author="Wolfram Research", title="{PoissonDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonDistribution.html}", note=[Accessed: 14-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_poissondistribution, organization={Wolfram Research}, title={PoissonDistribution}, year={2007}, url={https://reference.wolfram.com/language/ref/PoissonDistribution.html}, note=[Accessed: 14-December-2025]}