SkellamDistribution
SkellamDistribution[μ1,μ2]
represents a Skellam distribution with shape parameters μ1 and μ2.
Details
- The probability for integer value
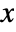in a Skellam distribution is proportional to ![(mu_1/mu_2)^(x/2) TemplateBox[{x, {2, , {sqrt(, {{mu, _, 1}, , {mu, _, 2}}, )}}}, BesselI]](Files/SkellamDistribution.en/2.png "(mu_1/mu_2)^(x/2) TemplateBox[{x, {2, , {sqrt(, {{mu, _, 1}, , {mu, _, 2}}, )}}}, BesselI]")
. - SkellamDistribution[μ1,μ2] is the distribution for
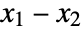where the 
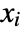are independent Poisson distributed with parameter μi. - SkellamDistribution allows μ1 and μ2 to be any positive real numbers.
- SkellamDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- SkellamDistribution[μ1,μ2] represents a discrete statistical distribution defined for integer values
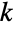, which is determined by the positive real parameters μ1 and μ2 and is defined as the distribution of the difference XY1-Y2, where Y1PoissonDistribution[μ1] and Y2PoissonDistribution[μ2] are independent variates with means μ1 and μ2, respectively. The Skellam distribution has a probability density function (PDF) that is discrete and unimodal and whose overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of μ1 and μ2. - The Skellam distribution was first derived by J. G. Skellam in the mid-1940s as the theoretical distribution modeling the difference of two Poisson-distributed variates from different populations. Since then, the distribution has been used in image analysis to study image differences in the presence of ambient noise as well as differences in the number of accidents between two locations and/or two periods of time. The Skellam distribution has also been used to model phenomena including sports scoring, stock prices, queueing models, and gene expression.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Skellam distribution. Distributed[x,SkellamDistribution[μ1,μ2]], written more concisely as xSkellamDistribution[μ1,μ2], can be used to assert that a random variable x is distributed according to a Skellam distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[SkellamDistribution[μ1,μ2],x] and CDF[SkellamDistribution[μ1,μ2],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Skellam distribution, EstimatedDistribution to estimate a Skellam parametric distribution from given data, and FindDistributionParameters to fit data to a Skellam distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Skellam distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Skellam distribution.
- TransformedDistribution can be used to represent a transformed Skellam distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Skellam distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Skellam distributions.
- SkellamDistribution is related to a number of other statistical distributions. It is a transformation (TransformedDistribution) of PoissonDistribution in the sense that SkellamDistribution[μ1,μ2] is equivalent to the distribution of x-y where xPoissonDistribution[μ1] and yPoissonDistribution[μ2]. SkellamDistribution is also closely related to PoissonConsulDistribution, CompoundPoissonDistribution, and PolyaAeppliDistribution.
Examples
open allclose allScope (7)
Generate a sample of pseudorandom numbers from a Skellam distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Applications (3)
The CDF of SkellamDistribution is an example of a right-continuous function:
The Chicago Cubs and St. Louis Cardinals scored an average of 4.72 and 4.88 runs per game, respectively, between the 2004 and 2008 seasons. Assume the runs for each team are independent and distributed according to a PoissonDistribution with the mean, respectively:
The point spread distribution:
Compute the probability that the Cardinals will score at least 2 more runs than the Cubs in a game:
The expected margin of victory, given the Cubs beat the Cardinals by more than 1 run:
The number of packets arriving to a loading dock follows a PoissonDistribution with mean 30 per hour. The packets are then removed from the dock following a PoissonDistribution with mean 25 per hour. Find the distribution of the number of packets remaining on the dock:
Simulate the number of packets on the dock for the next 100 hours:
Text
Wolfram Research (2010), SkellamDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/SkellamDistribution.html.
CMS
Wolfram Language. 2010. "SkellamDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SkellamDistribution.html.
APA
Wolfram Language. (2010). SkellamDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SkellamDistribution.html