CompoundPoissonDistribution[λ,dist]
represents a compound Poisson distribution with rate parameter λ and jump size distribution dist.


CompoundPoissonDistribution
CompoundPoissonDistribution[λ,dist]
represents a compound Poisson distribution with rate parameter λ and jump size distribution dist.
Details
- CompoundPoissonDistribution is also known as a stopped‐sum distribution.
- The compound Poisson distribution is equivalent to
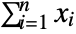 , where
, where 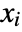 are independent and identically distributed random variables following dist and nPoissonDistribution[λ].
are independent and identically distributed random variables following dist and nPoissonDistribution[λ]. - CompoundPoissonDistribution allows λ to be any positive real number and dist to be any univariate distribution.
- CompoundPoissonDistribution can be used with such functions as Mean, Variance, and RandomVariate.
Background & Context
- CompoundPoissonDistribution[λ,dist] represents a discrete statistical distribution parameterized by a positive real number λ and a univariate distribution dist, the latter of which can be either discrete or continuous. The compound Poisson distribution models the sum of
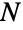 independent and identically distributed random variables
independent and identically distributed random variables 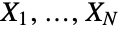 , where Xidist for all
, where Xidist for all 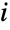 and NPoissonDistribution[λ]. The parameters λ and dist determine all properties possessed by the probability density function (PDF) of a compound Poisson distribution, including its shape, height, location, and domain. The compound Poisson distribution is referred to by a variety of other terms, including Poisson-stopped sum, generalized Poisson distribution, multiple Poisson distribution, composed Poisson distribution, stuttering Poisson distribution, clustered Poisson distribution, Pollaczek–Geiringer distribution, and Poisson power series distribution.
and NPoissonDistribution[λ]. The parameters λ and dist determine all properties possessed by the probability density function (PDF) of a compound Poisson distribution, including its shape, height, location, and domain. The compound Poisson distribution is referred to by a variety of other terms, including Poisson-stopped sum, generalized Poisson distribution, multiple Poisson distribution, composed Poisson distribution, stuttering Poisson distribution, clustered Poisson distribution, Pollaczek–Geiringer distribution, and Poisson power series distribution. - The study of the compound Poisson process (under the name of Pollaczek–Geiringer distributions) dates back to the 1930s. In its infancy, the compound Poisson distribution was devised as a tool to model the statistical behavior of "rare events," including accidents, diseases, and suicides. Within the study of stochastic processes, the compound Poisson distribution is also the motivation behind the so-called Bernoulli process, a continuous-time stochastic process with jumps whose sizes are randomly distributed according to a specified distribution and in which the jumps arrive according to a Poisson process. More recently, stopped sum distributions such as the compound Poisson distribution have been used to model a variety of phenomena, including the types/frequencies of insurance claims and the frequencies/amounts of rainfall.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a compound Poisson distribution. Distributed[x,CompoundPoissonDistribution[λ,dist]], written more concisely as xCompoundPoissonDistribution[λ,dist] , can be used to assert that a random variable x is distributed according to a compound Poisson distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[CompoundPoissonDistribution[λ,dist],x] and CDF[CompoundPoissonDistribution[λ,dist],x], though the PDF (as well as "PDF-related" quantities such as HazardFunction and Likelihood) will be undefined whenever dist is a continuous distribution. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively and are defined for either continuous or discrete dist.
- DistributionFitTest can be used to test if a given dataset is consistent with a compound Poisson distribution, EstimatedDistribution to estimate a compound Poisson parametric distribution from given data, and FindDistributionParameters to fit data to a compound Poisson distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic compound Poisson distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic compound Poisson distribution.
- TransformedDistribution can be used to represent a transformed compound Poisson distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a compound Poisson distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving compound Poisson distributions.
- CompoundPoissonDistribution is related to a number of other statistical distributions and constructs. CompoundPoissonDistribution is a generalization of PoissonDistribution, and because of the allowance of the parameter dist to take on any univariate distribution, there exists a generic relationship between CompoundPoissonDistribution and the collection of all univariate distributions in the Wolfram Language. In a less abstract sense, CompoundPoissonDistribution is a slice distribution of CompoundPoissonProcess in the sense that CompoundPoissonProcess[λ,dist][t] simplifies to CompoundPoissonDistribution[t λ,dist]. In addition, several distributions within the Wolfram Language can be derived via CompoundPoissonDistribution[λ,dist] for various values of dist, e.g. BinomialDistribution (when dist is BernoulliDistribution) and NegativeBinomialDistribution (when dist is LogSeriesDistribution).
Examples
open all close allBasic Examples (2)
Scope (7)
Simulate a compound Poisson distribution for different renewal rates:
Distribution parameter estimation:
Estimate the distribution parameters from sample data:
Compare the histogram of the data with a sample from the estimated distribution:
Define a compound Poisson distribution:
Define a compound Poisson distribution:
Compare to the reward distribution:
Compare to the renewal distribution:
Different moments with closed forms as functions of parameters:
Generating functions for a CompoundPoissonDistribution:
Factorial moment generating function:
Compound Poisson distribution with a mixture jump distribution:
Applications (2)
Shoppers arrive at a newly renovated store according to a Poisson process with a rate of 20 customers per hour. The store promotes this event by giving every customer a gift. The gift has a value that follows a Weibull distribution with shape parameter 10 and scale parameter 3. Find the expected total cost of the gifts given by the store during the 12-hour period for which the store is open on that day:
Expected total cost of the gifts given on the inaugural day:
Probability that the store spends between $500 and $800 on the gifts:
Aggregate claims from a risk have a compound Poisson distribution with Poisson parameter 200 and an individual claim amount distribution, which is a Pareto distribution with minimum value parameter 300, shape parameter 3, and location parameter 0. The insurer has effected excess of loss reinsurance with retention level $300. Calculate the mean and variance of the reinsurer's aggregate claims. The individual claims for the reinsurer follow a transformed Pareto distribution, since the reinsurer only pays amounts greater than $300:
Properties & Relations (5)
CompoundPoissonDistribution is a slice distribution of CompoundPoissonProcess:
CompoundPoissonDistribution with BernoulliDistribution is a PoissonDistribution:
CompoundPoissonDistribution with a special BorelTannerDistribution follows PoissonConsulDistribution:
The sum of Borel–Tanner distributed variables follows the Borel–Tanner distribution, hence the slice distribution is equivalent to the parameter mixture distribution:
Compare characteristic functions:
Renewal rate influences the kurtosis:
Use a different reward distribution:
Slice of CompoundRenewalProcess with renewal time given by ExponentialDistribution:
Create a random sample for rate 3 and slice at 7:
Compare to a sample of the corresponding CompoundPoissonDistribution:
Related Guides
History
Text
Wolfram Research (2012), CompoundPoissonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html.
CMS
Wolfram Language. 2012. "CompoundPoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html.
APA
Wolfram Language. (2012). CompoundPoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html
BibTeX
@misc{reference.wolfram_2025_compoundpoissondistribution, author="Wolfram Research", title="{CompoundPoissonDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_compoundpoissondistribution, organization={Wolfram Research}, title={CompoundPoissonDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/CompoundPoissonDistribution.html}, note=[Accessed: 11-March-2026]}