PoissonConsulDistribution[μ,λ]
represents a Poisson–Consul distribution with parameters μ and λ.


PoissonConsulDistribution
PoissonConsulDistribution[μ,λ]
represents a Poisson–Consul distribution with parameters μ and λ.
Details
- PoissonConsulDistribution is also known as generalized Poisson distribution (GPD).
- The probability for integer value
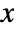 in a Poisson–Consul distribution is
in a Poisson–Consul distribution is 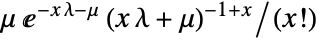 for
for 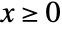 , and is zero for
, and is zero for 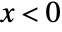 .
. - PoissonConsulDistribution allows μ to be any positive real number and λ to be any real number between 0 and 1.
- PoissonConsulDistribution allows μ and λ to be dimensionless quantities. »
- PoissonConsulDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- PoissonConsulDistribution[μ,λ] represents a discrete statistical distribution defined for integer values
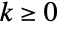 and determined by the real parameters μ (
and determined by the real parameters μ (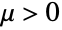 ) and λ (
) and λ (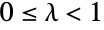 ). The Poisson-Consul distribution has a probability density function (PDF) that is discrete and unimodal. The distribution is sometimes also referred to as the generalized Poisson distribution or GPD due to the fact that "the" Poisson distribution (PoissonDistribution) may be realized as a special case, and is also sometimes referred to as the Lagrangian Poisson distribution.
). The Poisson-Consul distribution has a probability density function (PDF) that is discrete and unimodal. The distribution is sometimes also referred to as the generalized Poisson distribution or GPD due to the fact that "the" Poisson distribution (PoissonDistribution) may be realized as a special case, and is also sometimes referred to as the Lagrangian Poisson distribution. - The Poisson-Consul distribution is a generalization of the standard Poisson distribution (named after French mathematician Siméon Poisson) and bears the name of statistician Prem C. Consul who worked on the generalized distribution throughout the 1970s and 1980s. Like the classical Poisson distribution, the Poisson-Consul distribution is extremely useful in modeling situations consisting of a large number of independent trials with very small probability of occurrence (e.g. the number of deaths per year of cavalry soldiers stemming from kicks by horse) and extends the classical Poisson distribution in the sense that the probability of occurrence of a single event need remain constant. The Poisson-Consul distribution has also been used to model a number of modern phenomena such as domestic violence, and is a valuable modeling tool in areas such as finance and actuarial science.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Poisson-Consul distribution. Distributed[x,PoissonConsulDistribution[μ,λ]], written more concisely as xPoissonConsulDistribution[μ,λ], can be used to assert that a random variable x is distributed according to a Poisson-Consul distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[PoissonConsulDistribution[μ,λ],x] and CDF[PoissonConsulDistribution[μ,λ],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Poisson-Consul distribution, EstimatedDistribution to estimate a Poisson-Consul parametric distribution from given data, and FindDistributionParameters to fit data to a Poisson-Consul distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Poisson-Consul distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Poisson-Consul distribution.
- TransformedDistribution can be used to represent a transformed Poisson-Consul distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Poisson-Consul distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Poisson-Consul distributions.
- PoissonConsulDistribution is related to a number of other statistical distributions. It is an immediate generalization of PoissonDistribution in that the PDF of PoissonConsulDistribution[μ,0] is precisely the same as that of PoissonDistribution[μ]. In addition, PoissonConsulDistribution can be realized as a parameter mixture (ParameterMixtureDistribution) of BorelTannerDistribution while PoissonConsulDistribution[μ,λ] limits to InverseGaussianDistribution as μ→∞ (provided that μ (1-λ) remains fixed). PoissonConsulDistribution is also related to PascalDistribution, BinomialDistribution, NegativeBinomialDistribution, MultinomialDistribution, and NegativeMultinomialDistribution.
Examples
open all close allScope (8)
Generate a sample of pseudorandom numbers from a Poisson–Consul distribution:
Compare sample histogram to the PDF of the Poisson-Consul distribution:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
For large μ, the distribution becomes symmetric:
For large μ, the kurtosis becomes close to the kurtosis of NormalDistribution:
Different moments with closed forms as functions of parameters:
Use dimensionless Quantity to define PoissonConsulDistribution:
Applications (3)
CDF of PoissonConsulDistribution is an example of a right-continuous function:
The number of customers arriving at a service desk follows PoissonDistribution with mean 0.6, and the number of customers already in line before the service desk opens follows PoissonDistribution with mean 5. The number of customers served until there is no one in line follows PoissonConsulDistribution:
Plot the probability mass function:
Expected number of customers served:
Find the probability that at least 15 customers will be served at a busy period:
Simulate numbers of customers served at 30 busy periods:
The initial size of a population has PoissonDistribution with mean μ. The size of each offspring generation is also Poisson distributed with mean proportional to the generation size, with constant λ. Simulate the total progeny:
The total progeny follows a PoissonConsulDistribution:
Properties & Relations (5)
The sum of random variates from PoissonConsulDistribution with the same λ parameter follows PoissonConsulDistribution with the same λ parameter:
Proof using factorial moment-generating functions:
Relationships to other distributions:
Poisson–Consul distribution simplifies to PoissonDistribution:
The limit of large μ in PoissonConsulDistribution such that ![]() is fixed gives InverseGaussianDistribution:
is fixed gives InverseGaussianDistribution:
PoissonConsulDistribution is a parameter mixture of BorelTannerDistribution and PoissonDistribution:
Related Guides
Text
Wolfram Research (2010), PoissonConsulDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "PoissonConsulDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html.
APA
Wolfram Language. (2010). PoissonConsulDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html
BibTeX
@misc{reference.wolfram_2025_poissonconsuldistribution, author="Wolfram Research", title="{PoissonConsulDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_poissonconsuldistribution, organization={Wolfram Research}, title={PoissonConsulDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PoissonConsulDistribution.html}, note=[Accessed: 09-March-2026]}