NegativeBinomialDistribution[n,p]
represents a negative binomial distribution with parameters n and p.


NegativeBinomialDistribution
NegativeBinomialDistribution[n,p]
represents a negative binomial distribution with parameters n and p.
Details

- The probability for value
 in a negative binomial distribution is
in a negative binomial distribution is  for non-negative integers, and is zero otherwise. »
for non-negative integers, and is zero otherwise. » - NegativeBinomialDistribution allows n to be any non-negative real number and p to be any positive real number less than or equal to 1.
- If n is a positive integer, NegativeBinomialDistribution[n,p] gives the distribution of the number of failures in a sequence of trials with success probability p before n successes occur.
- NegativeBinomialDistribution for noninteger parameter n is also known as Pólya distribution.
- NegativeBinomialDistribution allows n and p to be a dimensionless quantity. »
- NegativeBinomialDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- NegativeBinomialDistribution[n,p] represents a discrete statistical distribution defined for integer values
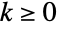 and determined by the positive real parameters n and p (where
and determined by the positive real parameters n and p (where 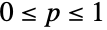 ). The negative binomial distribution has a probability density function (PDF) that is discrete and unimodal. Depending on context, the Pascal and Pólya–Aeppli distributions (PascalDistribution and PolyaAeppliDistribution, respectively) may each be referred to as negative binomial distributions, though each is distinct from the negative binomial distribution discussed above.
). The negative binomial distribution has a probability density function (PDF) that is discrete and unimodal. Depending on context, the Pascal and Pólya–Aeppli distributions (PascalDistribution and PolyaAeppliDistribution, respectively) may each be referred to as negative binomial distributions, though each is distinct from the negative binomial distribution discussed above. - When n is a positive integer, NegativeBinomialDistribution[n,p] gives the distribution of the number of failures in a sequence of trials with success probability p before n successes occur. This is closely related to the Pascal distribution (PascalDistribution) and dates back to Pascal's work in the 17
 century. For noninteger parameter n, the negative binomial distribution is also known as the Pólya distribution. For general n, several distributions dating to the 1940s have been proposed and referred to as negative binomial distributions, though the above-stated NegativeBinomialDistribution (which was proposed considerably later) is the most widely used in modern applications. The negative binomial distribution has played an increasingly significant role in probability and stochastics since the 1990s and has also been used to model phenomena including accident statistics, birth-and-death processes, consumer expenditure, biometrics, and retail inventory management.
century. For noninteger parameter n, the negative binomial distribution is also known as the Pólya distribution. For general n, several distributions dating to the 1940s have been proposed and referred to as negative binomial distributions, though the above-stated NegativeBinomialDistribution (which was proposed considerably later) is the most widely used in modern applications. The negative binomial distribution has played an increasingly significant role in probability and stochastics since the 1990s and has also been used to model phenomena including accident statistics, birth-and-death processes, consumer expenditure, biometrics, and retail inventory management. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a negative binomial distribution. Distributed[x,NegativeBinomialDistribution[n,p]] , written more concisely as xNegativeBinomialDistribution[n,p], can be used to assert that a random variable x is distributed according to a negative binomial distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for negative binomial distributions may be given using PDF[NegativeBinomialDistribution[n,p]] and CDF[NegativeBinomialDistribution[n,p]]. The mean, median, variance, covariance, raw moments, and central moments may be computed using Mean, Median, Variance, Covariance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a negative binomial distribution, EstimatedDistribution to estimate a negative binomial parametric distribution from given data, and FindDistributionParameters to fit data to a negative binomial distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic negative binomial distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic negative binomial distribution.
- TransformedDistribution can be used to represent a transformed negative binomial distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a negative binomial distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving negative binomial distributions.
- NegativeBinomialDistribution is related to a number of other distributions. It is a univariate case of the more general NegativeMultinomialDistribution in the sense that the PDF of NegativeBinomialDistribution[n,p] with respect to a variable x is precisely the same as that of NegativeMultinomialDistribution[n,{1-p}] written in terms of the vector {x}. NegativeBinomialDistribution[1,p] is identically GeometricDistribution[p], while NegativeBinomialDistribution can be obtained as a transformed distribution (TransformedDistribution) of both PascalDistribution and GeometricDistribution. Using a parameter mixture distribution (ParameterMixtureDistribution), NegativeBinomialDistribution can be realized from PoissonDistribution, GammaDistribution, BetaDistribution, and BetaPrimeDistribution, while also being related to CompoundPoissonDistribution via more complex transformations. NegativeBinomialDistribution is also related to BinomialDistribution, MultinomialDistribution, BernoulliDistribution, BetaBinomialDistribution, HypergeometricDistribution, and PoissonDistribution.
Examples
open all close allScope (8)
Generate a sample of pseudorandom numbers from a negative binomial distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
For large n, the distribution becomes more symmetric:
For large values of n, kurtosis gets close to the kurtosis of the standard NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Use dimensionless Quantity to define NegativeBinomialDistribution:
Applications (7)
The CDF of NegativeBinomialDistribution is an example of a right-continuous function:
The number of tails before getting 4 heads with a fair coin:
Plot the distribution of tail counts:
Compute the probability of getting at least 6 tails before getting 4 heads:
Compute the expected number of tails before getting 4 heads:
A coin was flipped 10 times and the 8![]() head occurred at the 10
head occurred at the 10![]() flip. Find the probability of such an event if the coin is fair:
flip. Find the probability of such an event if the coin is fair:
Assuming the coin may not be fair, find the most likely value for ![]() :
:
A basketball player shoots free throws until he hits 4 of them. His probability of scoring in any one of them is 0.7. Simulate the process:
Find the number of shots the player is expected to shoot:
Find the probability that the player requires 4 shots:
Assume the probability of fouling for each minute interval is 0.1 independently. Simulate the fouling process for 30 minutes:
A basketball player fouls out after 6 fouls. Find the expected playing time until foul out:
A shipment of products is inspected in batches of 60 and each batch is inspected up to rejection when the 10![]() defective item is found. Find the probability of a batch being rejected if 20% of the items are defective:
defective item is found. Find the probability of a batch being rejected if 20% of the items are defective:
Alternatively, compute the same result by truncating the distribution:
Simulate the number of non-defective products in rejected batches:
Illustrate the ratio in each batch:
Find the average ratio of non-defective to defective products in rejected batches:
A data stream containing ![]() data packets is repeatedly sent without order information. Find the distribution of the number of unordered data stream arrivals until all the packets arrive in the right order for the second time:
data packets is repeatedly sent without order information. Find the distribution of the number of unordered data stream arrivals until all the packets arrive in the right order for the second time:
Find the probability that packets will arrive the second time in the correct order after at most 18 fails:
Find the average number of fails until the second ordered data stream:
Simulate the number of fails until the second ordered data stream:
Properties & Relations (11)
NegativeBinomialDistribution[n,p] converges to a normal distribution when n->∞:
Negative binomial distribution is closed under addition:
The limit of negative binomial distribution when the mean is fixed is PoissonDistribution:
Relationships to other distributions:

Negative binomial distribution simplifies to GeometricDistribution:
Negative binomial distribution and PascalDistribution differ by a shift:
Sum of n independent variables from GeometricDistribution has negative binomial distribution:
General proof for an arbitrary number of sum components:
A univariate NegativeMultinomialDistribution is a negative binomial distribution:
NegativeBinomialDistribution is a mixture of PoissonDistribution and GammaDistribution:
BetaNegativeBinomialDistribution is a mixture of negative binomial distribution and BetaDistribution:
A limit of zero-truncated NegativeBinomialDistribution is a LogSeriesDistribution:
Possible Issues (2)
NegativeBinomialDistribution is not defined when n is non-positive:
NegativeBinomialDistribution is not defined when p is not between zero and one:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Text
Wolfram Research (2007), NegativeBinomialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "NegativeBinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html.
APA
Wolfram Language. (2007). NegativeBinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html
BibTeX
@misc{reference.wolfram_2025_negativebinomialdistribution, author="Wolfram Research", title="{NegativeBinomialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html}", note=[Accessed: 20-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_negativebinomialdistribution, organization={Wolfram Research}, title={NegativeBinomialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/NegativeBinomialDistribution.html}, note=[Accessed: 20-January-2026]}