BetaBinomialDistribution[α,β,n]
represents a beta binomial mixture distribution with beta distribution parameters ![]() and
and ![]() , and
, and ![]() binomial trials.
binomial trials.


BetaBinomialDistribution
BetaBinomialDistribution[α,β,n]
represents a beta binomial mixture distribution with beta distribution parameters ![]() and
and ![]() , and
, and ![]() binomial trials.
binomial trials.
Details
- BetaBinomialDistribution is also known as a Pólya distribution and as a negative hypergeometric distribution.
- The beta binomial distribution is a binomial distribution with n trials whose probability parameter
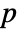 follows a beta distribution with shape parameters α and β. »
follows a beta distribution with shape parameters α and β. » - BetaBinomialDistribution allows α and β to be any positive real numbers, and n to be any positive integer.
- BetaBinomialDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- BetaBinomialDistribution[α,β,n] represents a discrete statistical distribution defined at integer values
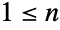 , where the parameters α, β are positive real numbers known as shape parameters, which determine the overall shape and behavior of the probability density function (PDF). In general, the beta binomial distribution has a discrete PDF, and depending on the values of α and β, the PDF may have monotonically increasing values, values that have a single "peak" or "valley" within the interior of its domain, or may be uniform. The beta binomial distribution is sometimes referred to as a Pólya distribution or as a negative hypergeometric distribution.
, where the parameters α, β are positive real numbers known as shape parameters, which determine the overall shape and behavior of the probability density function (PDF). In general, the beta binomial distribution has a discrete PDF, and depending on the values of α and β, the PDF may have monotonically increasing values, values that have a single "peak" or "valley" within the interior of its domain, or may be uniform. The beta binomial distribution is sometimes referred to as a Pólya distribution or as a negative hypergeometric distribution. - The beta binomial distribution can be thought of as an abstraction of the Bernoulli (BernoulliDistribution) and binomial (BinomialDistribution) distributions in which the success probability p of a known number of Bernoulli trials is random, and the associated binomial distribution has success probability p, which follows the beta distribution (BetaDistribution). In Bayesian terms, this means that the beta binomial distribution arises as a posterior predictive distribution of a binomial variable in which the prior distribution on the success probability p is a beta distribution. The first documented application of the beta binomial distribution dates back to the work of Hugo Muench on probabilistic modeling of medical trials in the 1930s, and even today, a number of real world phenomena can be modeled by a beta binomial distribution. For example, the beta binomial distribution can be utilized in the Pólya urn model for a specific set of drawing and replacement rules. More recently, beta binomial distributions have been used to assess the performance of biometric identification devices, in the study of Bayesian networks, and in various artificial intelligence algorithms.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a beta binomial distribution. Distributed[x,BetaBinomialDistribution[α,β,n]], written more concisely as xBetaBinomialDistribution[α,β,n], can be used to assert that a random variable x is distributed according to a beta binomial distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BetaBinomialDistribution[α,β,n],x] and CDF[BetaBinomialDistribution[α,β,n],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a beta binomial distribution, EstimatedDistribution to estimate a beta binomial parametric distribution from given data, and FindDistributionParameters to fit data to a beta binomial distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic beta binomial distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic beta binomial distribution.
- TransformedDistribution can be used to represent a transformed beta binomial distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a beta binomial distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving beta binomial distributions.
- BetaBinomialDistribution is related to a number of other statistical distributions. As previously mentioned, BetaBinomialDistribution combines features from both BinomialDistribution and BetaDistribution, a fact made precise by observing that ParameterMixtureDistribution[BinomialDistribution[n,p],pBetaDistribution[α,β]] evaluates to BetaBinomialDistribution[α,β,n]. Similarly, DiscreteUniformDistribution[{0,n}] is precisely the same as BetaBinomialDistribution[1,1,n], a fact that subsequently induces qualitative links with UniformDistribution, TriangularDistribution, and PERTDistribution. In a very natural way, BetaBinomialDistribution is related to BetaNegativeBinomialDistribution, and because of the fact that MultinomialDistribution and DirichletDistribution are higher-dimensional analogues of BinomialDistribution and BetaDistribution, respectively, BetaBinomialDistribution can be viewed as a one-dimensional analog of the so-called Dirichlet-multinomial distribution.
Examples
open all close allScope (7)
Generate a sample of pseudorandom numbers from a beta binomial distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Assuming known n, estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Applications (4)
The probability of more than 50 successes in 100 trials assuming a beta distribution on ![]() :
:
Define a negative hypergeometric distribution:
Find the probability that ![]() black balls were sampled without replacement before a
black balls were sampled without replacement before a ![]()
![]() white ball was drawn from an urn initially filled with
white ball was drawn from an urn initially filled with ![]() black and
black and ![]() white balls:
white balls:
Alternatively, compute the probability of drawing a white ball provided that there were ![]() black balls in the previous
black balls in the previous ![]() samplings without replacement:
samplings without replacement:
Define the Pólya distribution:
Define the Pólya–Eggenberg urn distribution:
The distribution models an urn scheme. An urn contains ![]() white balls and
white balls and ![]() black balls. When a ball is drawn it is returned to the urn together with
black balls. When a ball is drawn it is returned to the urn together with ![]() additional balls of the same color. The distribution gives the probability of drawing
additional balls of the same color. The distribution gives the probability of drawing ![]() white balls in
white balls in ![]() draws:
draws:
Properties & Relations (5)
The probability of getting negative integers, integers beyond n, or noninteger numbers is zero:
Relationships to other distributions:
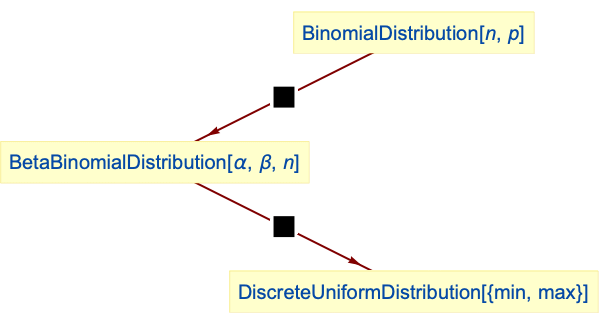
DiscreteUniformDistribution is a special case of a beta binomial distribution:
For ![]() and
and ![]() , the beta binomial distribution has a triangular shape but is not a discrete version of TriangularDistribution:
, the beta binomial distribution has a triangular shape but is not a discrete version of TriangularDistribution:
Confirm that the preceding expression gives the PDF of ![]() where
where ![]() follows a TriangularDistribution:
follows a TriangularDistribution:
BetaBinomialDistribution is a mixture of BinomialDistribution and BetaDistribution:
Possible Issues (3)
BetaBinomialDistribution is not defined when α or β is non-positive:
BetaBinomialDistribution is not defined when n is not a positive integer:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
History
Text
Wolfram Research (2007), BetaBinomialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html.
CMS
Wolfram Language. 2007. "BetaBinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html.
APA
Wolfram Language. (2007). BetaBinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html
BibTeX
@misc{reference.wolfram_2025_betabinomialdistribution, author="Wolfram Research", title="{BetaBinomialDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_betabinomialdistribution, organization={Wolfram Research}, title={BetaBinomialDistribution}, year={2007}, url={https://reference.wolfram.com/language/ref/BetaBinomialDistribution.html}, note=[Accessed: 25-February-2026]}