PERTDistribution[{min,max},c]
represents a PERT distribution with range min to max and mode at c.
PERTDistribution[{min,max},c,λ]
represents a modified PERT distribution with shape parameter λ.


PERTDistribution
PERTDistribution[{min,max},c]
represents a PERT distribution with range min to max and mode at c.
PERTDistribution[{min,max},c,λ]
represents a modified PERT distribution with shape parameter λ.
Details

- PERTDistribution is used for project completion time analysis within PERT (program evaluation and review technique) and is effectively a reparametrized BetaDistribution.
- PERTDistribution is also known as beta-PERT distribution.
- PERTDistribution[{min,max},c,λ] is equivalent to TransformedDistribution[min+x(max-min),xBetaDistribution[1+λ
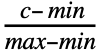 ,1+λ
,1+λ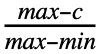 ]].
]]. - PERTDistribution allows min, max, and c to be any real numbers such that min<c<max and λ is any non-negative real number.
- PERTDistribution allows min, max, and c to be any quantities of the same unit dimensions, and λ to be a dimensionless quantity. »
- PERTDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- PERTDistribution represents a smooth, potentially skewed version of a uniform or triangle distribution (implemented in the Wolfram Language as UniformDistribution and TriangularDistribution, respectively) that has a single peak and is defined on a finite interval. More precisely, PERTDistribution[{min,max},c,λ] represents a statistical distribution defined for values between min and max that is parametrized by two constants c and λ≥0. Here, c is the mode of the distribution and thus determines the horizontal location of the peak of its probability density function (PDF), while λ is a "shape parameter" that (together with c) determines the overall shape of the PDF. The two-argument form PERTDistribution[{min,max},c] is equivalent to PERTDistribution[{min,max},c,4].
- "PERT" is an acronym for "project evaluation and review techniques", a name that refers to the large-scale use of the distribution in the modeling of expert estimates of a desired quantity (e.g. project completion time) given an expert's guesses for the minimum, maximum, and most likely values of that quantity. The PERT distribution is sometimes referred to as the beta-PERT distribution.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a PERT distribution. Distributed[x,PERTDistribution[{min,max},c,λ]], written more concisely as xPERTDistribution[{min,max},c,λ], can be used to assert that a random variable x is distributed according to a PERT distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[PERTDistribution[{min,max},c,λ],x] and CDF[PERTDistribution[{min,max},c,λ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a PERT distribution, EstimatedDistribution to estimate a PERT parametric distribution from given data, and FindDistributionParameters to fit data to a PERT distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic PERT distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic PERT distribution.
- TransformedDistribution can be used to represent a transformed PERT distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a PERT distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving PERT distributions.
- PERTDistribution is closely related to a number of other distributions. For example, the PERT distribution is defined to be a transformed BetaDistribution (more precisely, PERTDistribution[{min,max},c,λ] is equivalent to TransformedDistribution[min+x(max-min),xBetaDistribution[1+λ
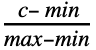 ,1+λ
,1+λ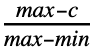 ]]) and can be used as a smooth alternative to TriangularDistribution. Due to its close relationship with BetaDistribution, PERTDistribution can be viewed as a less-direct generalization of both UniformDistribution and PowerDistribution. Like BetaDistribution, PERTDistribution can be obtained via transformations of KumaraswamyDistribution and NoncentralBetaDistribution; also like BetaDistribution, PERTDistribution is closely related to PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
]]) and can be used as a smooth alternative to TriangularDistribution. Due to its close relationship with BetaDistribution, PERTDistribution can be viewed as a less-direct generalization of both UniformDistribution and PowerDistribution. Like BetaDistribution, PERTDistribution can be obtained via transformations of KumaraswamyDistribution and NoncentralBetaDistribution; also like BetaDistribution, PERTDistribution is closely related to PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
Examples
open all close allBasic Examples (5)
Scope (8)
Generate a sample of pseudorandom numbers from a PERT distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
For large λ, the modified PERT distribution becomes symmetric:
For large λ, kurtosis nears the kurtosis of NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
An expert estimates that a project that takes from 4 to 6 months to complete will take 5 months and 1 week:
The distribution of the project completion time:
Find the expected completion time and its standard deviation:
Find the probability of the project taking longer to complete:
Use PERTDistribution as a smooth alternative to TriangularDistribution:
Properties & Relations (5)
PERT distribution is closed under translation and scaling by a positive factor:
Relationships to other distributions:
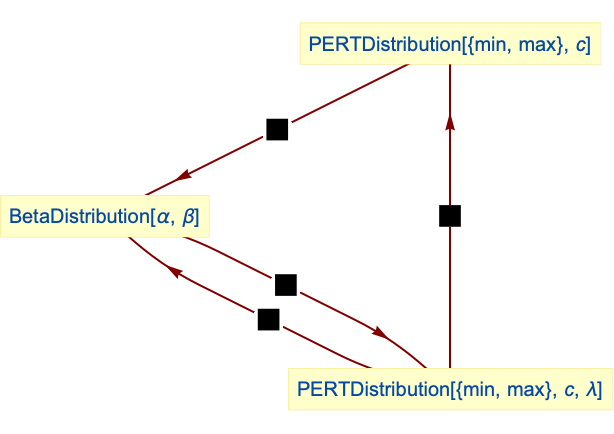
Default value of the shape parameter λ is 4:
PERT distribution is a transformation of BetaDistribution:
BetaDistribution with parameters ![]() and
and ![]() is a special case of PERTDistribution on the unit interval:
is a special case of PERTDistribution on the unit interval:
See Also
Related Guides
Text
Wolfram Research (2010), PERTDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PERTDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "PERTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PERTDistribution.html.
APA
Wolfram Language. (2010). PERTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PERTDistribution.html
BibTeX
@misc{reference.wolfram_2025_pertdistribution, author="Wolfram Research", title="{PERTDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PERTDistribution.html}", note=[Accessed: 26-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_pertdistribution, organization={Wolfram Research}, title={PERTDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PERTDistribution.html}, note=[Accessed: 26-January-2026]}