NoncentralBetaDistribution[α,β,δ]
represents a noncentral beta distribution with shape parameters α, β and noncentrality parameter δ.


NoncentralBetaDistribution
NoncentralBetaDistribution[α,β,δ]
represents a noncentral beta distribution with shape parameters α, β and noncentrality parameter δ.
Details
- The probability density for value
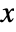 in a noncentral beta distribution is proportional to
in a noncentral beta distribution is proportional to ![x^(alpha-1)(1-x)^(beta-1) TemplateBox[{{alpha, +, beta}, alpha, {{(, {x, , delta}, )}, /, 2}}, Hypergeometric1F1] x^(alpha-1)(1-x)^(beta-1) TemplateBox[{{alpha, +, beta}, alpha, {{(, {x, , delta}, )}, /, 2}}, Hypergeometric1F1]](Files/NoncentralBetaDistribution.en/2.png) for
for 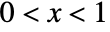 , and is zero for
, and is zero for 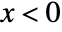 or
or 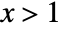 .
. - NoncentralBetaDistribution allows α, β, and δ to be any positive real numbers.
- NoncentralBetaDistribution allows α, β, and δ to be dimensionless quantities.
- NoncentralBetaDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- NoncentralBetaDistribution[α,β,δ] represents a continuous statistical distribution supported over the interval
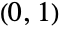 and parametrized by positive real numbers α, β, and δ (two "shape parameters" and a "noncentrality parameter", respectively), which together determine the overall behavior of its probability density function (PDF). NoncentralBetaDistribution is a perhaps-skewed generalization of the BetaDistribution (sometimes referred to as the centralized beta distribution), and while it is most often referred to as "the" noncentral beta distribution, a number of other noncentral generalizations of the beta distribution also exist.
and parametrized by positive real numbers α, β, and δ (two "shape parameters" and a "noncentrality parameter", respectively), which together determine the overall behavior of its probability density function (PDF). NoncentralBetaDistribution is a perhaps-skewed generalization of the BetaDistribution (sometimes referred to as the centralized beta distribution), and while it is most often referred to as "the" noncentral beta distribution, a number of other noncentral generalizations of the beta distribution also exist. - NoncentralBetaDistribution is the distribution of the quotient
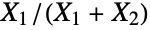 when exactly one of
when exactly one of 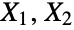 is a noncentral chi-square (NoncentralChiSquareDistribution) random variate. It is therefore analogous to the BetaDistribution, which models the quotient
is a noncentral chi-square (NoncentralChiSquareDistribution) random variate. It is therefore analogous to the BetaDistribution, which models the quotient 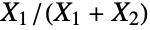 for chi-square (ChiSquareDistribution) random variates
for chi-square (ChiSquareDistribution) random variates 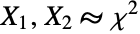 . While the distribution was first derived in the 1920s, its detailed properties were first studied in the 1950s by statistician J. L. Hodges. Since then, the distribution has been used to model a variety of phenomena, including coherence between pairs of signals in signal analysis and asset exchange returns in finance.
. While the distribution was first derived in the 1920s, its detailed properties were first studied in the 1950s by statistician J. L. Hodges. Since then, the distribution has been used to model a variety of phenomena, including coherence between pairs of signals in signal analysis and asset exchange returns in finance. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a noncentral beta distribution. Distributed[x,NoncentralBetaDistribution[α,β,δ]], written more concisely as xNoncentralBetaDistribution[α,β,δ], can be used to assert that a random variable x is distributed according to a noncentral beta distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for noncentral beta distributions may be given using PDF[NoncentralBetaDistribution[α,β,δ],x] and CDF[NoncentralBetaDistribution[α,β,δ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a noncentral beta distribution, EstimatedDistribution to estimate a noncentral beta parametric distribution from given data, and FindDistributionParameters to fit data to a noncentral beta distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic noncentral beta distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic noncentral beta distribution.
- TransformedDistribution can be used to represent a transformed noncentral beta distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a noncentral beta distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving noncentral beta distributions.
- NoncentralBetaDistribution is related to a number of other distributions. It is an immediate generalization of BetaDistribution, in the sense that the PDF of NoncentralBetaDistribution[α,β,δ] tends to that of BetaDistribution[α,β] as δ→0. NoncentralBetaDistribution can be realized as a transformation of both NoncentralFRatioDistribution and NoncentralChiSquareDistribution and is also closely related to PERTDistribution, PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
Examples
open all close allBasic Examples (3)
Scope (6)
Generate a sample of pseudorandom numbers from a noncentral beta distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Applications (1)
Properties & Relations (4)
Relationships to other distributions:
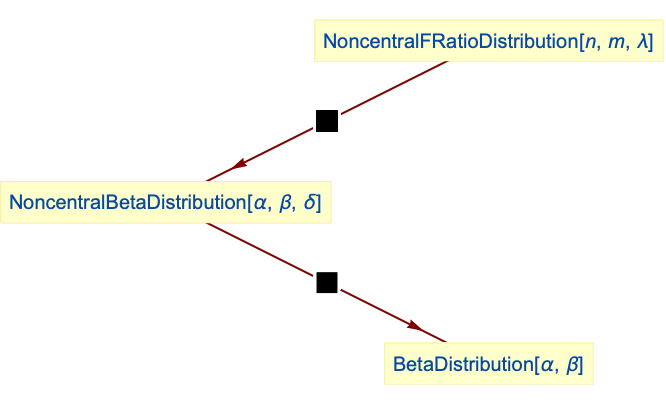
With noncentrality parameter δ going to 0, this is BetaDistribution:
NoncentralBetaDistribution is a transformation of NoncentralFRatioDistribution:
NoncentralBetaDistribution can be obtained as a transformation of ChiSquareDistribution and NoncentralChiSquareDistribution:
Related Guides
Text
Wolfram Research (2010), NoncentralBetaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "NoncentralBetaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html.
APA
Wolfram Language. (2010). NoncentralBetaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html
BibTeX
@misc{reference.wolfram_2025_noncentralbetadistribution, author="Wolfram Research", title="{NoncentralBetaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_noncentralbetadistribution, organization={Wolfram Research}, title={NoncentralBetaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/NoncentralBetaDistribution.html}, note=[Accessed: 26-February-2026]}